Законы изменения давления в зазоре
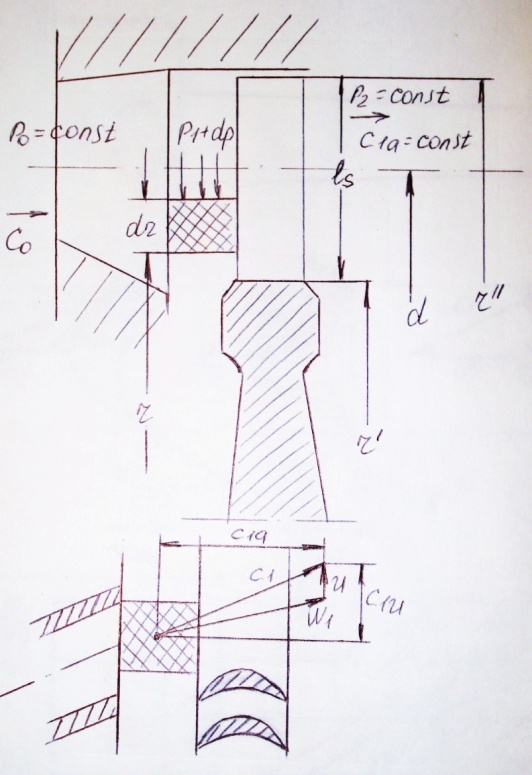
Для этого рассмотрим элементарную частицу газа массой dm, высотой dr и площадью df в момент выхода ее из направляющего канала на радиусе r. Поскольку в окружном направлении частица движется со скоростью С1u, то центробежная сила, приложенная к этой частице, будет
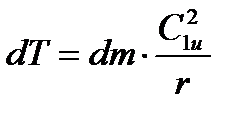
или
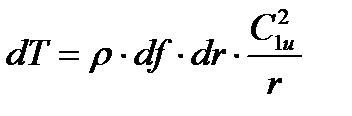
Полагаем, что в зазоре нет радиального течения. Тогда сила dТ уравновешивается разностью давлений Р1 и Р1 + dР, приложенных к частице.
Условие равновесия запишется в виде (т.к. радиальные составляющие скорости равны нулю)
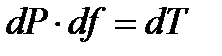
или
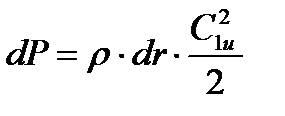
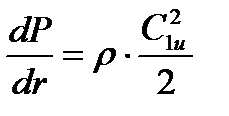
Это уравнение показывает закон изменения статического давления в зазоре по радиусу между соплом и лопаткой.
41. Закрутка лопатки по закону постоянной циркуляции или по закону свободного вихря (r·Cu = const)
Данный закон закрутки лопаток получил наибольшее распространение при профилировании турбинных, компрессорных и вентиляторных ступеней.
В его основу положено представление о безвихревом течении потока перед и за рабочей лопаткой. При таком безвихревом течении предполагается, что осевые составляющие абсолютных скоростей перед лопаткой С1а и за лопаткой С2а остаются постоянными на всех радиусах по высоте лопатки. Следовательно и полное давление за и перед рабочими лопатками постоянно.
Кроме того, в этом методе предполагается, что радиальная составляющая скорости потока равна нулю Сr = 0. Это означает, что перетекание потока вдоль лопатки отсутствует. Окружная работа Lu в каждом сечении лопатки одинакова, т.е.
C1a = const; C2a = const; P*2 = const; Lu = const;
Основное дифференциальное уравнение течения потока в этом случае запишется так
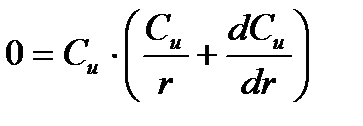
или, полагая, Cu ≠ 0 получим
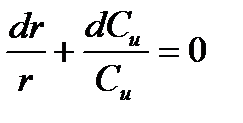
интегрируя, найдем
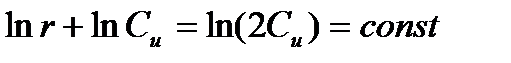
откуда
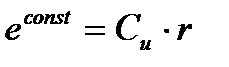 и
и 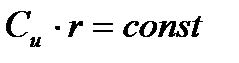
Следовательно, заданное течение можно организовать в том случае, если изменение окружных составляющих будет пропорционально радиусу, т.е.
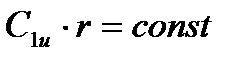 ;
; 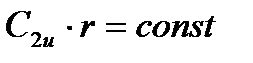
Это соотношение выражает известный гидродинамике «закон площадей» или закон постоянства циркуляции Г по высоте лопатки ( 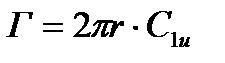 ) и соответствует закону распределения скоростей в свободном вихре.
) и соответствует закону распределения скоростей в свободном вихре.
Поэтому рассматриваемый метод профилирования длинных лопаток называется методом постоянной циркуляции. Основоположником этого метода является Н.Е. Жуковский, применивший его для профилирования воздушных винтов и лопаток вентилятора. В 1945 г. Этот метод был применен профессором В.В. Уваровым к расчету длинных лопаток. Особенно благоприятные результаты дал этот метод в применении к лопаткам газовых турбин.
Основным преимуществом ступени, выполненной в соответствии с законом постоянной циркуляции, является постоянство удельной работы, развиваемой рабочим колесом во всех цилиндрических сечениях ступени и постоянство полной энергии в пространстве за рабочим колесом.
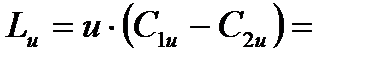
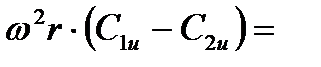
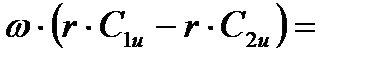
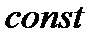 ;
; 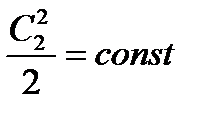
Входные и выходные треугольники скоростей для трех радиусов по высоте лопатки показаны на рисунке.
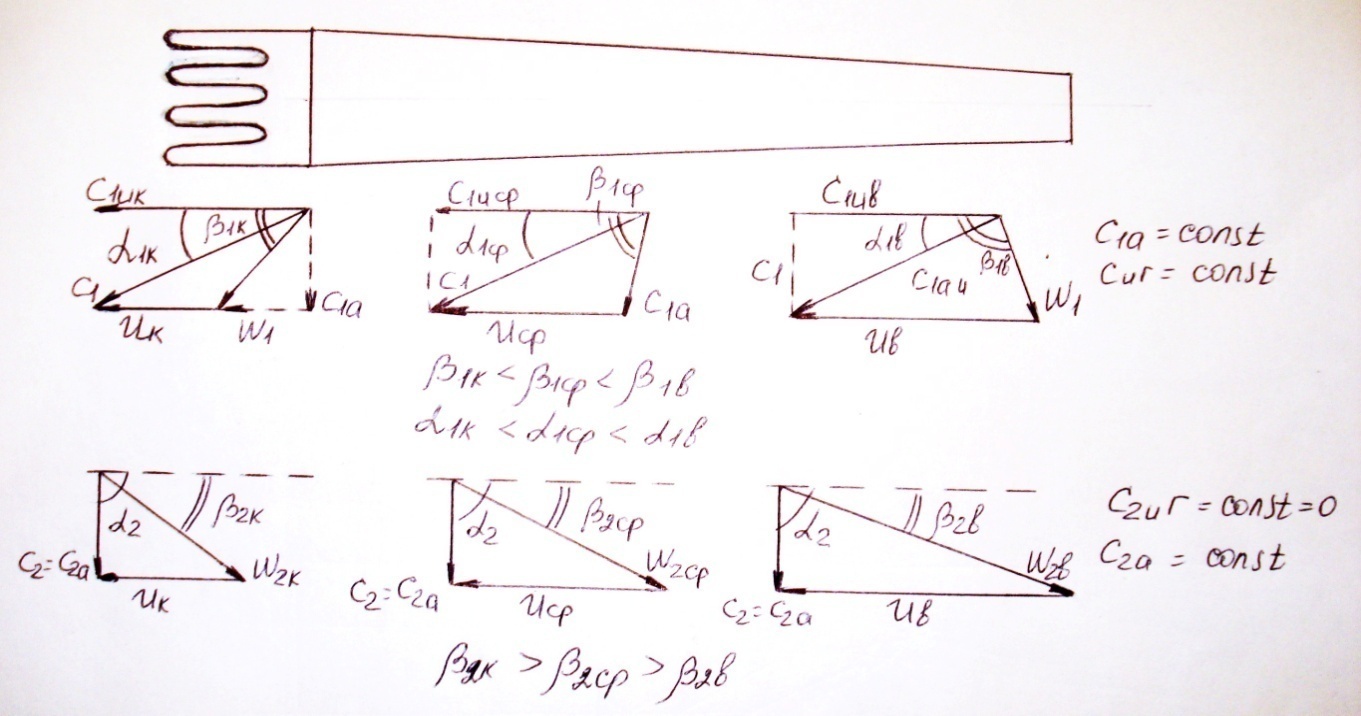
В соответствии с законом постоянства момента скорости, т.е. 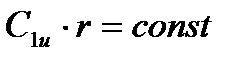 , составляющая абсолютной скорости С1u получается max у корня и минимальной у вершины. Поскольку осевая составляющая абсолютной скорости С1а остается постоянной, то углы потока α1 и β1 должны возрастать от корня к вершине лопатки.
, составляющая абсолютной скорости С1u получается max у корня и минимальной у вершины. Поскольку осевая составляющая абсолютной скорости С1а остается постоянной, то углы потока α1 и β1 должны возрастать от корня к вершине лопатки.
При выходе из рабочего колеса в силу закона 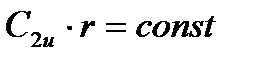 относительная скорость W2 получается наибольшей у вершины лопатки, где окружная скорость имеет максимальное значение. У корня лопатки W2 имеет наименьшее значение. Поэтому угол β2 должен увеличиваться от вершины лопатки к его корню. Т.о., в ступени постоянной циркуляции требуется закрутка как направляющих, так и рабочих лопаток.
относительная скорость W2 получается наибольшей у вершины лопатки, где окружная скорость имеет максимальное значение. У корня лопатки W2 имеет наименьшее значение. Поэтому угол β2 должен увеличиваться от вершины лопатки к его корню. Т.о., в ступени постоянной циркуляции требуется закрутка как направляющих, так и рабочих лопаток.
Проектирование и изготовление таких лопаток представляется достаточно затруднительным. Поэтому в целях упрощения профиля лопаток были предложены другие виды закруток лопаток, отличающиеся от закрутки по закону постоянной циркуляции.
На основании уравнения 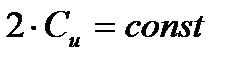 можно найти скорости и углы в любом радиальном сечении лопатки, если только они известны в каком либо сечении.
можно найти скорости и углы в любом радиальном сечении лопатки, если только они известны в каком либо сечении.
При построении профиля обычно считают известными величины скоростей и углов или на среднем диаметре или у корневого сечения лопаток.
Пусть нам известны величины скоростей и углов у корневого сечения, тогда для любого другого сечения имеем из уравнения 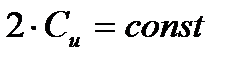
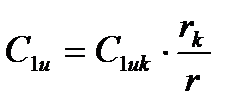 (1)
(1)
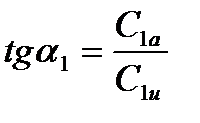 (2)
(2)
По условию вывода уравнения 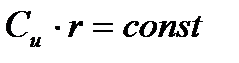
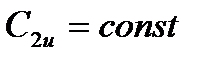 , тогда с учетом (1), получим
, тогда с учетом (1), получим
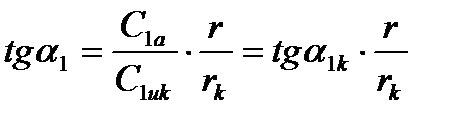 (3)
(3)
Следовательно, угол потока при выходе из направляющих каналов растет с увеличением радиуса.
Скорость 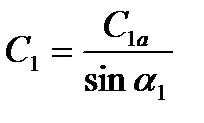 (4)
(4)
Угол входа потока на лопатку
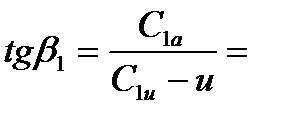
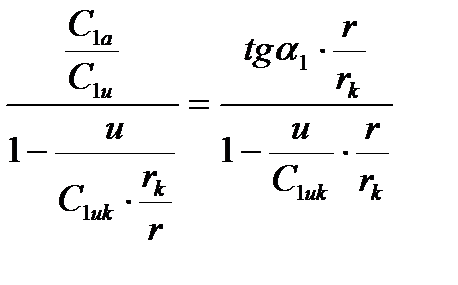 (5)
(5)
В выходном треугольнике
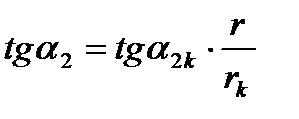 (6)
(6)
 , отсюда следует, что α2 = 90°
, отсюда следует, что α2 = 90°
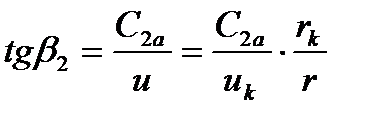 (7)
(7)
т.е. с увеличением радиуса β2 уменьшается.
Поскольку поток за рабочими лопатками не закручен (  ), то статическое давление Р2 будет приблизительно постоянным по всей высоте лопатки.
), то статическое давление Р2 будет приблизительно постоянным по всей высоте лопатки.
В зазоре же между соплом и рабочей лопаткой статическое давление Р1 увеличивается от корня лопатки к периферии. В связи с этим будет изменяться величина теплоперепада has, срабатываемого на различных радиусах рабочей лопатки. Отсюда следует, что при постоянстве теплоперепада ha, срабатываемого на всей ступени степень реакции 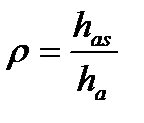 будет возрастать от корня к периферии. Лопатка, выполненная у корня со степенью реактивности ρ = 0, у вершины будет иметь положительную реактивность.
будет возрастать от корня к периферии. Лопатка, выполненная у корня со степенью реактивности ρ = 0, у вершины будет иметь положительную реактивность.
Изменение степени реактивности по сечениям следует определять по найденным для каждого сечения скоростям C и W.
При этом
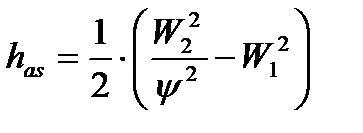
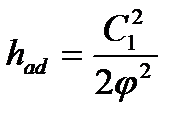
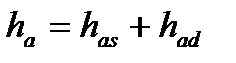
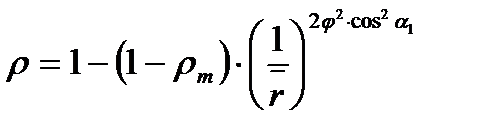
где 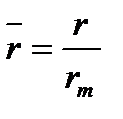 , r – текущий радиус, rm - средний радиус
, r – текущий радиус, rm - средний радиус
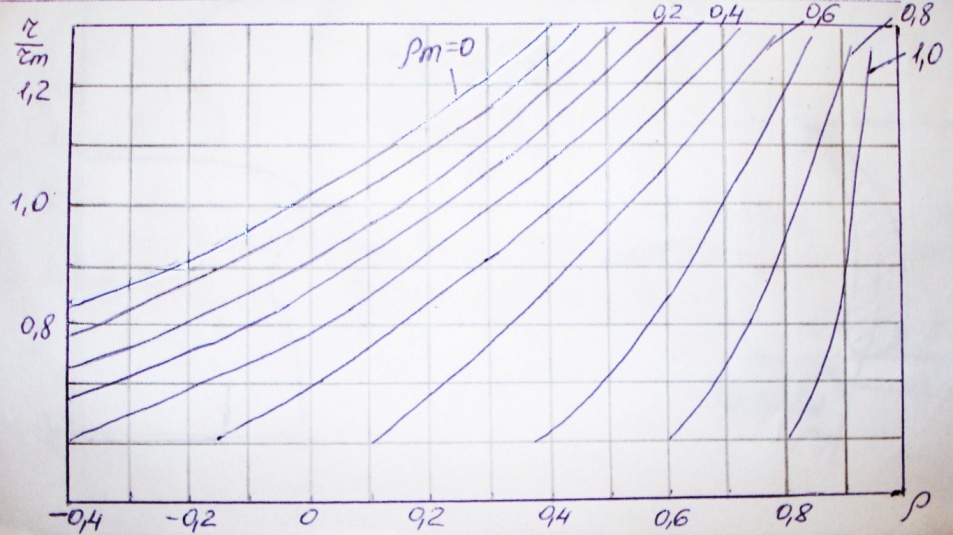
Реактивность на любом радиусе зависит в основном от 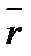 и исходной реактивности
и исходной реактивности 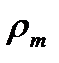 на среднем радиусе. Заметное влияние оказывает угол выхода из сопел, как фактор определяющий закрутку потока и, следовательно, после центробежных сил.
на среднем радиусе. Заметное влияние оказывает угол выхода из сопел, как фактор определяющий закрутку потока и, следовательно, после центробежных сил.
При 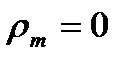 получается существенная положительная реактивность в периферийной области и отрицательная реактивность в корневой. В областях ступени с отрицательной реактивностью происходит сжатие потока в колесе, необходимая для этого энергия черпается из кинетической энергии потока на выходе из сопел, что снижает к.п.д. ступени. Для исключения областей с отрицательной реактивностью достаточно положить у корня
получается существенная положительная реактивность в периферийной области и отрицательная реактивность в корневой. В областях ступени с отрицательной реактивностью происходит сжатие потока в колесе, необходимая для этого энергия черпается из кинетической энергии потока на выходе из сопел, что снижает к.п.д. ступени. Для исключения областей с отрицательной реактивностью достаточно положить у корня 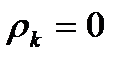 .
.
При значительной положительной реактивности у корня в ступенях большой верности реактивность у периферии велика, что вызывает большую перетечку рабочего тела через радиальный зазор, при отсутствии бандажа, кроме того, из канала в канал.
Для оценки 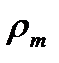 при желаемой реактивности у корня можно пользоваться уравнением
при желаемой реактивности у корня можно пользоваться уравнением
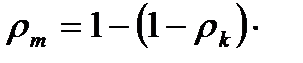
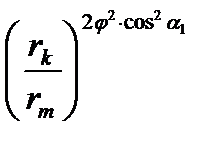
Из формулы и рисунка следует, что реактивность остается постоянной вдоль радиуса только при 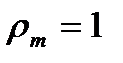 . Этот случай предельный, когда весь теплоперепад ступени срабатывается в рабочем колесе. При этом отсутствует перепад в соплах
. Этот случай предельный, когда весь теплоперепад ступени срабатывается в рабочем колесе. При этом отсутствует перепад в соплах 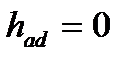 , нет поля центробежных сил перед колесом и, следовательно, реактивность постоянна.
, нет поля центробежных сил перед колесом и, следовательно, реактивность постоянна.
42. Закрутка по закону α1 = const (закрутка Эпперта)
Технологически трудно выполнять закрученными рабочие и направляющие лопатки. Поэтому Эпперт предложил направляющие лопатки оставлять незакрученными (α1 = const). Тогда, пологая, α1 = const и ρ* = const из основного уравнения движения потока в зазоре между направляющими и рабочими лопатками можно написать
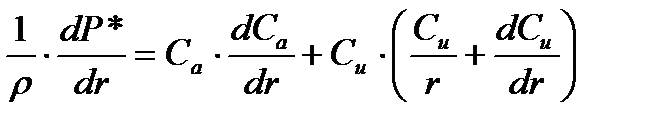
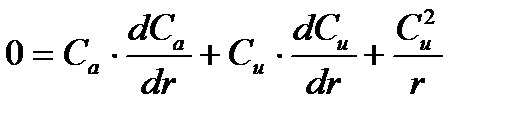 , умножим на dr, тогда
, умножим на dr, тогда

Рассмотрим
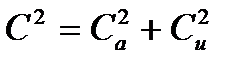
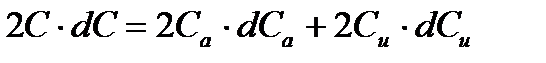
Тогда
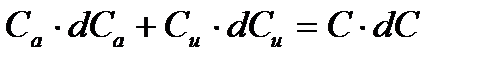
или
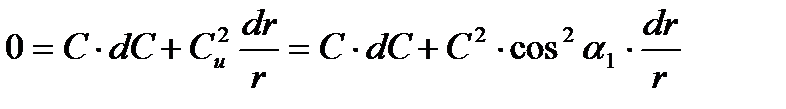 , сокращая на С2 получим
, сокращая на С2 получим
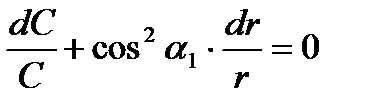 , интегрируя, найдем
, интегрируя, найдем
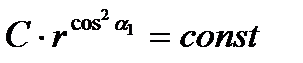
Но, т.к. 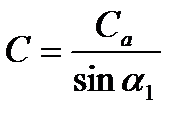 и
и 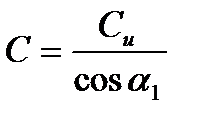 , то
, то
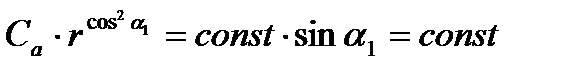
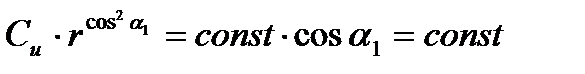
При закрутке Эпперта скорость С1 и ее составляющие С1а и С1u будут уменьшаться от корня к периферии.
Направляющие лопатки выполняются незакрученными, рабочие лопатки оказываются менее закрученными, чем при закрутке по закону Сur = const.
Экономичность турбинной ступени с закрученными лопатками получается заметно выше, чем экономичность ступени с обычным цилиндрическим облапачиванием.
Исследования УКТИ показали, что при отношениях 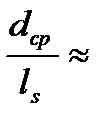 10 ÷ 11 уже следует применять закрученное облапачивание
10 ÷ 11 уже следует применять закрученное облапачивание
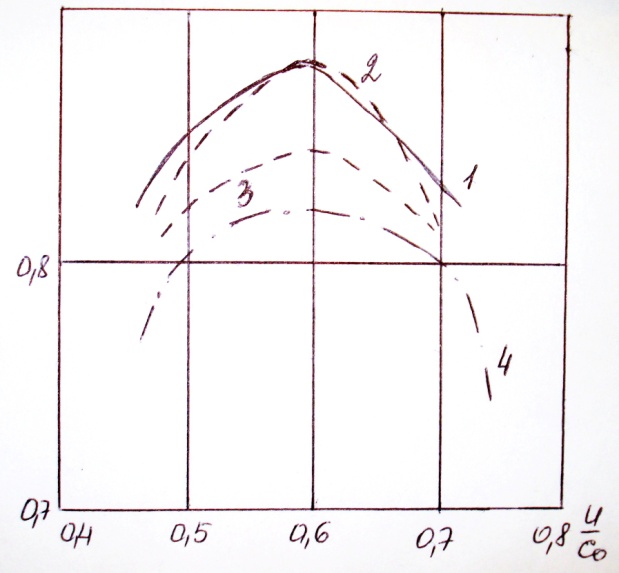
1-облапачивание, выполненное по закону Сur = const; Сa = const
2-по закону ρСa = const
3-с постоянной реакцией по радиусу
4-цилиндрические облапачивания (без закрутки).
Дата добавления: 2015-07-22; просмотров: 2528;
