Уравнение Эйлера для окружной работы

Поток рабочего тела перемещаясь вдоль криволинейного канала изменяет свое движение, т.е. в общем случае – величину и направление своей скорости. Поворот и ускорение струи пара в криволинейном канале возникают под влиянием:

- реактивного усилия стенок канала на струю пара

- разности давлений Р₁ – Р₂ при входе в канал и выходе из него

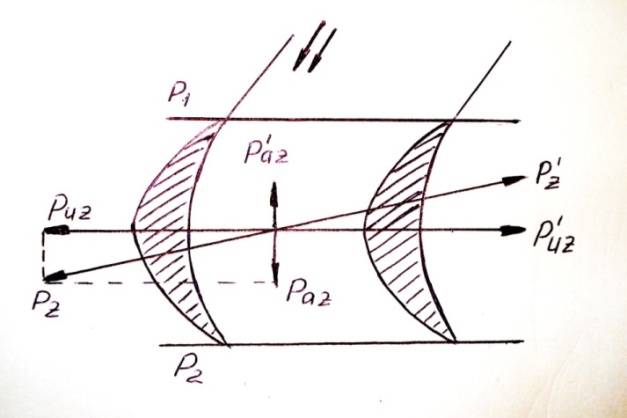
Равнодействующую всех усилий с которыми лопатка действует на паровую или газовую струю обозначим через P’z.

В соответствии с законами физики, струя пара будет оказывать на лопатку усилие Pz, равное но противоположное усилию P’z. При расчетах турбины обычно определяют не полное усилие струи, действующее на лопатку Pz, а его проекции на направление окружной скорости Puz и на перпендикулярное к ней осевое направление Paz. Наибольший интерес для нас представляет проекция Puz, т.к. она производит окружную работу.

Усилие, возникающее вследствие разности давлений Р₁ – Р₂ в направлении окружной скорости имеет проекцию, равную нулю.

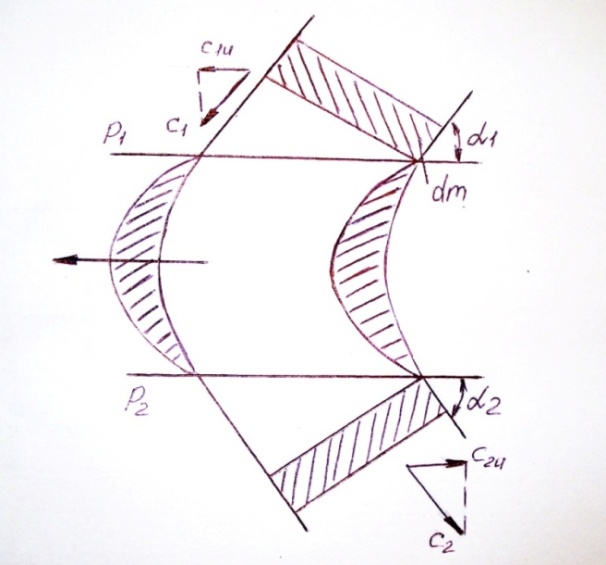
Окружная сила Puz найдется если к массе пара dm, протекающей через канал применить закон сохранения количества движения.

Пусть пар входит в канал с абсолютной скоростью С₁ и выходит из него со скоростью С₂ (она может быть направлена как угодно).

Элементарная масса пара, которая входит и выходит из канала за промежуток времени dt будет равна

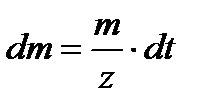
где z – количество лопаток на диске турбины; m – массовый расход вещества в кг/сек

Закон количества движения в этом случае может быть сформулирован в следующем виде:

проекция изменения вектора количества движения на направление окружной скорости равна импульсу силы, действующей на струю пара в этом направлении.

Тогда, принимая направление Puz за положительное, найдем

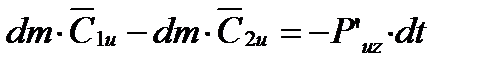
где С_1u – проекция абсолютной скорости C₁ на окружное направление; С_2u – проекция абсолютной скорости C₂ на окружное направление; -P’_uz – окружная составляющая силы действия стенки канала на струю.

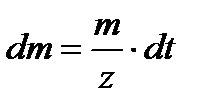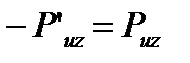Учитывая, что и что найдем

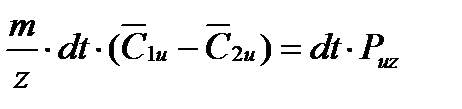
Откуда, окружная сила, действующая на одну лопатку

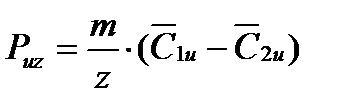(1)

Для всего рабочего колеса турбины при числе лопаток на нем z окружное усилие

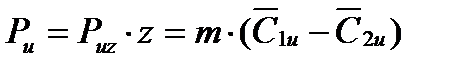(2)

Секундная работа, т.е. мощность, всей массы пара m на лопатках рабочего колеса турбины составит

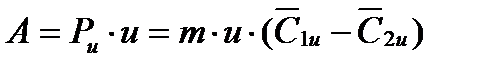, Дж/сек (3)

[кг/сек · м/сек · м/сек = кг·м/сек² · м/сек = Н·м/сек = Дж/сек]

Удельная работа, т.е. работа, отнесенная к 1кг/сек равна:

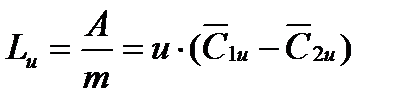, Дж/кг – уравнение Эйлера (1754 г) (4)

Аналогично может быть получено уравнение для проекции равнодействующей сил давлений пара в осевом направлении

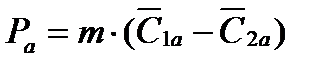
Здесь С_1а и С_2а всегда направлены в одну сторону.

Применяя уравнение Эйлера к осевой турбине можно определить величину вращательного момента, развиваемого паром на турбинном колесе

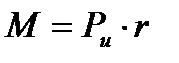
где r – средний радиус для выделенного канала или, в случае турбинной ступени, расстояние от середины лопаток до оси вращения.

Используя уравнение для Р_u, получим

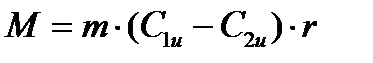
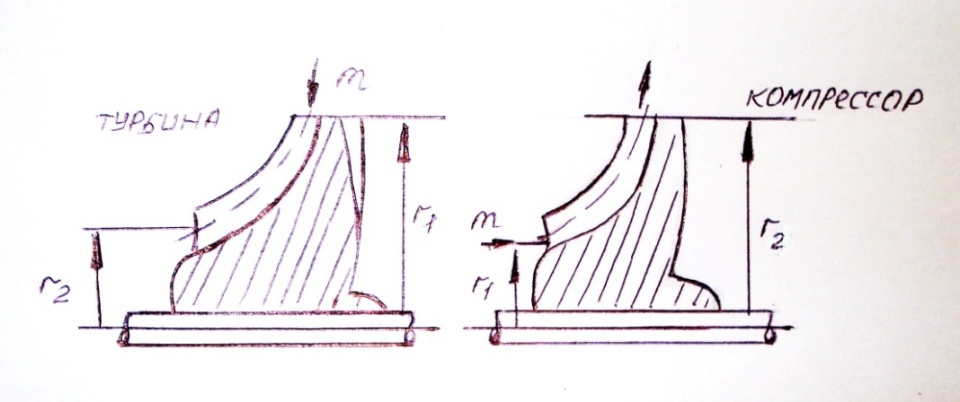
В том случае когда, средний радиус криволинейного канала при входе равен r₁ и при выходе из канала r₂ (как, например, в центробежном компрессоре или радиальной турбине), то для вычисления вращательного момента следует воспользоваться теоремой моментов количеств движения для системы материальных точек.

В соответствии с этой теоремой развиваемой паром момент на валу турбомашины будет равен изменению момента количества движения секундной массы.

Следовательно если на входе в рабочее колесо 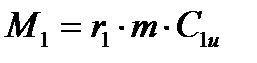, а на выходе из рабочего колеса 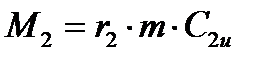, то момент на валу машины

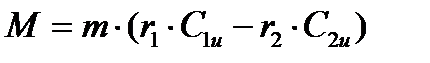
Мощность развиваемая турбинным колесом

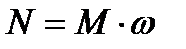или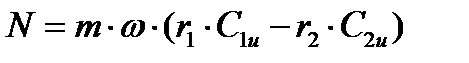

где ω – угловая скорость вращения