Взаимная рекурсия
Рекурсия позволяет определить единственный процесс как решение некоторого единственного уравнения. Эта техника легко обобщается на случай решения систем уравнений с более чем одним неизвестным. Для достижения желаемого результата необходимо, чтобы правые части всех уравнений были предваренными, а каждый неизвестный процесс входил ровно один раз в правую часть одного из уравнений.
Пример 3.4.Автомат с газированной водой имеет рукоятку с двумя возможными положениями — ЛИМОН и АПЕЛЬСИН. Действия по установке рукоятки в соответствующее положение назовем устлимон и устапельсин, а действия автомата по наливанию напитка — лимон иапельсин. Вначале рукоятка занимает некоторое нейтральное положение, к которому затем уже не возвращается. Ниже приводятся уравнения, определяющие алфавит и поведение трех процессов:
aАГАЗ = aG = aW = {устлимон, устапельсин, мон, лимон, апельсин}.
АГАЗ = (устлимон  G | устапельсин
G | устапельсин  W),
W),
G = (мон  лимон
лимон  G | устапельсин
G | устапельсин  W),
W),
W = (мон  апельсин
апельсин  W | устлимон
W | устлимон  G).
G).
Законы
Тождественность процессов с одинаковыми алфавитами можно устанавливать с помощью алгебраических законов, похожих на законы арифметики.
Первый закон касается оператора выбора. Он гласит, что два процесса, определенные с помощью оператора выбора, различны, если на первом шаге они предлагают различные альтернативы или после одинакового первого шага ведут себя по-разному. Если же множества начального выбора оказываются равными и для каждой начальной альтернативы дальнейшее поведение процессов совпадает, то, очевидно, что процессы тождественны.
L1.(х: А  Р(х)) = (у: В
Р(х)) = (у: В  Q(у)) º (А = В AND"х
Q(у)) º (А = В AND"х  А.Р(х) = Q(х))
А.Р(х) = Q(х))
Этот закон имеет ряд следствий:
L1A.СТОП 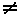 (a
(a  P).
P).
Доказательство.
ЛЧасть = (х: {}  P)
P) 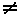 (х: {a}
(х: {a}  Р) = ПРЧасть, так как {}
Р) = ПРЧасть, так как {} 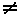 {a}.
{a}.
L1B.(с  Р) ≠ ( d
Р) ≠ ( d  Q), если с ≠ d.
Q), если с ≠ d.
Доказательство. Так как, {с} ≠ {d}.
L1C.(с  Р | d
Р | d  Q) = (d
Q) = (d  Q | с
Q | с  Р).
Р).
L1D.(с  Р) = (с
Р) = (с  Q) º Р = Q.
Q) º Р = Q.
Доказательство.Так как, {с} = {с}.
С помощью этих законов можно доказывать простые теоремы.
Пример 3.5. (мон  шок
шок  мон
мон  шок
шок  СТОП)
СТОП) 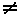 (мон
(мон  СТОП).
СТОП).
Доказательство. Следует из L1B и L1A.
Для доказательства более общих теорем о рекурсивно определенных процессах необходимо ввести закон, гласящий, что всякое должным образом предваренное рекурсивное уравнение имеет единственное решение.
L2.Если F(X) - предваренное выражение, то:
(Y = F(Y)) º (Y = mX.F(X)).
Как прямое следствие получаем, что mX.F(X) является решением соответствующего уравнения.
L2A.mX.F(X) = F(mX.F(X)).
Пример 3.6. Пусть ТА1 = (мон  ТА2), а ТА2 = (шок
ТА2), а ТА2 = (шок  ТА1). Требуется доказать, что ТА1 = ТАП.
ТА1). Требуется доказать, что ТА1 = ТАП.
Доказательство. ТА1 = (мон  ТА2) =по определению ТА1
ТА2) =по определению ТА1
= (мон  (шок
(шок  ТА1)) по определению ТА2
ТА1)) по определению ТА2
Таким образом, ТА1 является решением того же рекурсивного уравнения, что и ТАП. Так как это уравнение предварённое, оно имеет единственное решение. Значит, ТА1 = ТАП.
Дата добавления: 2015-07-18; просмотров: 1008;
