Прогнозирование в регрессионном анализе: интерполяция и экстраполяция
Применяя регрессионную модель для прогнозирования, необходимо учитывать лишь допустимые значения (relevant range) факторного признака (независимой переменной). В этот диапазон входят все значения переменной Х, начиная с минимального и заканчивая максимальным. Таким образом, предсказывая значение переменной У при конкретном значении переменной Х, исследователь выполняет интерполяцию между значениями переменной Х в диапазоне возможных значений. Однако экстраполяция за пределы этого интервала невозможна.
Например, пытаясь предсказать среднегодовой объем продаж в магазине, зная его площадь, мы можем вычислять значения переменной У лишь для значений переменной Х от1,1 до 5,8 тыс. кв. футов. Следовательно, прогнозировать среднегодовой объем продаж можно лишь для магазинов, площадь которых не выходит за пределы указанного диапазона.
Любая попытка экстраполяции означает, что мы предполагаем, что линейная регрессия сохраняет свой характер за пределами допустимого диапазона.
Вопрос 3. Непараметрические методы оценки корреляционной связи показателей.
На практике часто необходимо точно регистрировать не только количественные, но и качественные факторы.
При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, возможно использование "тетрахорических показателей".
Расчётная таблица для двух признаков состоит из четырёх ячеек (а,в,с,d). Каждая клетка соответствует альтернативе того и другого признака.
| Да | Нет | |
| Да | a | b |
| Нет | c | d |
Для анализа данных из таких таблиц построен ряд показателей:
- коэффициент ассоциации Д. Юла Кa :
Кa = 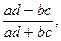 (26)
(26)
- коэффициент контингенции К.Пирсона Кк :
Кк = 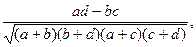 (27)
(27)
Коэффициент контингенции всегда находится в пределах от -1 до +1. Кроме того, значение коэффициента контингенции всегда меньше коэффициента ассоциации.
-1 < Кк < +1 ; Кк < Ка .
Применение понятий:
Проведен анализ «Исследование социальных аспектов трудовой деятельности работников торговых предприятий». Исследования по полу и содержанию работы представлены в таблице:
| Работа | Мужчины | Женщины | Всего |
| Интересная | 300 (а) | 201 (в) | 501 (а + в) |
| Неинтересная | 130 (с) | 252 (d) | 382 (с + d) |
| ИТОГО | 430 (а + с) | 453 (в + d) | 883 (а + в + с + d) |
Определить по данным таблицы коэффициент ассоциации.

По шкале Чеддока проверим Кa.
Вывод: имеет место средний размер связи, несмотря на разные мнения о своей работе у мужчин и женщин.
Для определения тесноты связи как между количественными, так и между качественными признаками (если значения признаков могут быть упорядочены, проранжированы по степени убывания или возрастания признака) можно использовать коэффициент корреляции рангов Спирмена rсп :
rсп=1 - 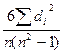 ,
,  (28)
(28)
где 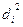 - квадраты разности рангов связанных величин х и у,
- квадраты разности рангов связанных величин х и у,
n - число наблюдений (число пар рангов).
Применение понятий:
Рассмотрим наличие связи между обеспеченностью товарной продукцией ряда предприятий (х) и накладными расходами по реализации (у). Значения х и у приведены в первых двух колонках следующей таблицы:
| x, | y, | Ранжирование | Разность рангов | di2 | |
| млн. руб. | тыс. руб. | Rx | Ry | di | |
| -1 | |||||
| 18,8 | -1 | ||||
| 11,0 | -1 | ||||
| 29,0 | |||||
| 17,5 | -1 | ||||
| 23,4 | |||||
| 35,6 | |||||
| 15,4 | -5 | ||||
| 26,1 | |||||
| 20,7 |
| ИТОГО |
Определим коэффициент Спирмена.
Необходимые величины для расчёта rсп найдены и записаны в колонках 3...6 таблицы, тогда:
rсп = 1 - 6*50/10*99 = 0,700
Вывод: выявленная связь (по шкале Чеддока) является заметной.
Если каждый качественный признак состоит более чем из двух групп, то для определения тесноты связи применяются:
коэффициент взаимной сопряженности К.Пирсона:
 (29)
(29)
Здесь φ2 - показатель взаимной сопряженности.
| Группы признака А | Группы признака В | Итого | ||
| Низкая В1 | Средняя В2 | Высокая В3 | ||
| А1 | f1 | f2 | f3 | n1 |
| А2 | f4 | f5 | f6 | n2 |
| А3 | f7 | f8 | f9 | n3 |
| Итого | m1 | m2 | m3 |
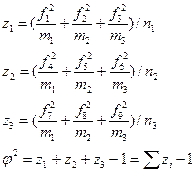 (30)
(30)
коэффициент взаимной сопряженности А.А.Чупрова:
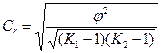 (31)
(31)
Здесь К1 - число групп по колонкам; К2 - число групп по строкам.
Коэффициент взаимной сопряженности А.А.Чупрова находится в пределах от 0 до 1. Это более точный коэффициент, по сравнению с коэффициентом взаимной сопряженности К.Пирсона, т.к. учитывает число групп по каждому признаку.
0 < Сr < +1
Чупров Александр Александрович (1874-1926) – русский теоретик статистики. С 1917г. проживал за границей.
Если надо найти тесноту связи между тремя и более признаками, то применяется ранговый коэффициент согласия - коэффициент конкордации W:
W = 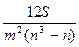 ,
,  (32)
(32)
где S - сумма квадратов отклонений рангов,
m - количество факторов,
n - число наблюдений.
Применение понятий:
Для десяти однотипных совместных предприятий известны следующие показатели:
| № СП | Реализация продукции, млн. у.е., у | Накладные расходы на реализацию, тыс. у.е., х | Себестоимость единицы продукции, 0,01 у.е., z | Средняя месячная зарплата работников, у.е., v |
| 12,0 | 68,8 | 168,5 | ||
| 18,8 | 70,2 | 158,7 | ||
| 11,0 | 71,4 | 171,7 | ||
| 29,0 | 78,5 | 183,9 | ||
| 17,5 | 66,9 | 160,4 | ||
| 23,9 | 69,7 | 165,2 | ||
| 35,6 | 72,3 | 175,0 | ||
| 15,4 | 77,5 | 170,4 | ||
| 26,1 | 65,2 | 162,7 | ||
| 20,7 | 70,7 | 163,0 |
Рассчитаем тесноту связи между указанными факторами с помощью коэффициента конкордации.
Выполняем вспомогательные расчеты, результаты которых представим в таблице.
Присваиваем ранги исходным данным:
| Ry | Rx | Rz | Rv | Сумма по строке | Квадраты сумм |
| å=220 | å=5590 |
S = 5590 - (220)2/10 = 5590 - 4840 = 750
W = (12*750) / (16*(1000-10)) = 0,57
Выводы:
Величина коэффициента конкордации показывает, что между исследуемыми величинами имеется тесная зависимость. Это объясняется тем, что все рассматриваемые величины являются показателями эффективности работы СП.
Дата добавления: 2015-07-18; просмотров: 1354;
