Джоулево тепло при сварке.
При пропускании тока в проводнике (рис.2.12) выделяется тепло, определяемое законом Джоуля-Ленца:
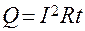 . (7)
. (7)
Полная тепловая мощность:
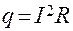 , (8)
, (8)
где I– ток, проходящий по проводнику;
R– сопротивление проводника.
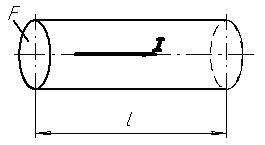
Рис. 2.12. Проводник с током.
Так как все тепло выделяется в проводнике и практически расходуется на его нагрев, то 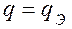 и
и  .
.
Тепло выделяется в каждой точке объема металла, т.е. имеем объемно распределенный источник нагрева. Найдем объемную плотность энергии:
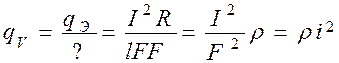 , (9)
, (9)
где: 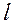 – длина проводника;
– длина проводника;
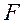 – поперечное сечение;
– поперечное сечение;
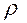 – удельное электрическое сопротивление;
– удельное электрическое сопротивление;
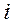 – плотность тока в проводнике.
– плотность тока в проводнике.
Известно, что 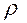 зависит от температуры Т:
зависит от температуры Т:
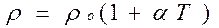 , (10)
, (10)
где: 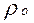 – удельное сопротивление при
– удельное сопротивление при 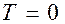 ;
;
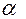 – температурный коэффициент электрического сопротивления.
– температурный коэффициент электрического сопротивления.
При сварке температура достигает значительной величины, поэтому 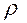 изменяется в широких пределах (см. табл. 2.4).
изменяется в широких пределах (см. табл. 2.4).
Таблица 2.4.
| Удельное электрическое сопротивление | Материал | |||
| Сталь 10 | Нержавеющая сталь | Медь | Д16Т | |
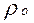 , Ом/см , Ом/см
| 15  10-6 10-6
| 70  10-6 10-6
| 1,75  10-6 10-6
| 5,8  10-6 10-6
|
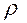 , Ом/см , Ом/см
| 110  10-6 10-6
| 120  10-6 10-6
| 5,75  10-6 10-6
| – |
Если в каком-либо объеме проводника температура повысится, то в этом объеме будет повышенное выделение тепла за счет увеличения 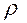 .
.
Джоулево тепло широко используют в сварочной технике. Применяя значительные плотности тока, можно при необходимости очень быстро (за тысячные доли секунды) нагреть металл до расплавления и осуществить сварку.
При сварке, как правило, имеется граница раздела между проводниками, которая несколько изменяет процессы выделения тепла. Граница раздела изменяет распределение тока. Из-за несовершенства контакта и наличия неровностей на поверхностях линии тока будут сужаться в определенных зонах (рис. 2.13.).
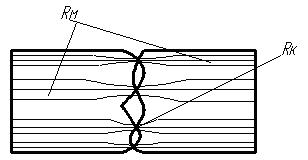
Рис. 2.13. Характер распределения линий тока при наличии границы раздела.
Сужение линий тока условно выражают введением дополнительного контактного сопротивления RК.
Тогда:
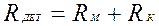 ,
,
где: 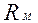 – сопротивление материала;
– сопротивление материала;
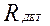 – полное сопротивление деталей.
– полное сопротивление деталей.
Следует отметить, что граница раздела не имеет существенного значения, если действует значительное сжимающее усилие (точечная или роликовая сварка, стыковая сварка с предварительным сжатием). В данном случае выступы очень быстро сминаются и линии тока равномерно распределяются по границе раздела. Основное тепло выделяется при этом в самом металле:
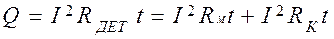 . (11)
. (11)
Второе слагаемое в балансе тепла составляет всего (5…10)%.
Значительную роль граница играет в случае, если сжимающее усилие отсутствует (стыковая сварка с предварительным оплавлением и др.). Тогда выступы и сужение линий тока сохраняются в течение всего процесса нагревания, и на границе раздела выделяется до 30% всего тепла, а в металле около 70%.
Джоулево тепло используют также при электрошлаковой сварке, когда ток пропускают через расплавленный электропроводный шлак, имеющий сопротивление RШ. В шлаке выделяется тепло:
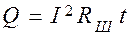 .
.
Температура шлака доводится до (1800…2200)оС (при сварке сталей). При такой температуре основной и присадочный металлы расплавляются и свариваются.
При индукционном нагреве с помощью тока высокой частоты (ТВЧ) (рис. 2.14.) в каждом замкнутом контуре проводника индуктируется ЭДС и по контуру проходит ток. Вследствие эффекта вытеснения ток главным образом проходит в поверхностном слое:
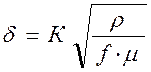 . (12)
. (12)
Здесь: 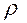 – удельное электросопротивление;
– удельное электросопротивление;
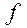 – частота тока;
– частота тока;
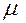 – магнитная проницаемость;
– магнитная проницаемость;
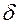 – глубина поверхностного слоя, где выделяется 90% всего тепла.
– глубина поверхностного слоя, где выделяется 90% всего тепла.
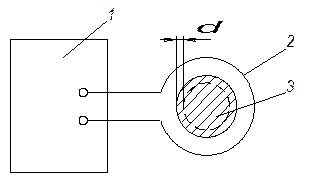
Рис. 2.14. Схема нагрева образца с помощью ТВЧ:
1 – источник ТВЧ; 2 – индуктор;
3 – нагреваемая заготовка.
Величина 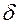 , мм, приведена в табл. 2.5.
, мм, приведена в табл. 2.5.
Табл. 2.5.
| Глубина поверхностного слоя | Материал | ||
| Низкоуглеродистая сталь при Т=20оС | Низкоуглеродистая сталь при Т=800оС | Медь | |
при 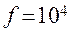 Гц Гц
| 0,2 | 6,5 | 0,67 |
при 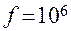 Гц Гц
| 0,02 | 0,65 | 0,067 |
Из таблицы видно, что величина 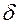 незначительна, т.е. можно считать, что нагрев ТВЧ – поверхностный. Глубинные слои металла нагреваются благодаря теплопроводности. Поэтому нагрев идет значительно медленнее, чем при обычном прохождении тока через металл.
незначительна, т.е. можно считать, что нагрев ТВЧ – поверхностный. Глубинные слои металла нагреваются благодаря теплопроводности. Поэтому нагрев идет значительно медленнее, чем при обычном прохождении тока через металл.
Потери тепла на нагрев индуктора и в окружающую среду составляют около половины всей мощности, поэтому 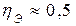 .
.
2.9 Основные законы, используемые для определения
температуры при сварке.
Рассмотрим некоторые общие вопросы нагрева заготовок с использованием различных источников тепла. Чтобы в полном объеме охарактеризовать нагрев свариваемых деталей, необходимо найти температурное поле Т=f(x,y,z,t) нагреваемого тела, где Т – температура любой точки тела, зависящая от координат точки и от времени. При определении температур используют следующие величины, понятия и законы:
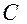 – удельная теплоемкость, Дж/г град;
– удельная теплоемкость, Дж/г град;
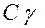 – объемная теплоемкость, Дж/см3.град;
– объемная теплоемкость, Дж/см3.град;
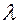 – коэффициент теплопроводности, Дж/см.с.град;
– коэффициент теплопроводности, Дж/см.с.град;
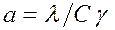 – коэффициент температуропроводности, см2/с;
– коэффициент температуропроводности, см2/с;
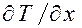 ,
, 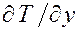 ,
, 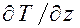 – градиент температуры в данном направлении.
– градиент температуры в данном направлении.
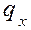 ,
, 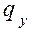 ,
, 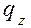 – плотность теплового потока в данном направлении.
– плотность теплового потока в данном направлении.
При нагреве тела тепло передается от более нагретых участков к менее нагретым посредством теплопроводности. Количество тепла 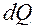 , проходящее через элементарную площадку
, проходящее через элементарную площадку 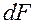 за время
за время 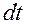 , равно:
, равно:
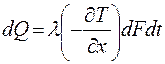 .
.
Обычно это равенство выражают в виде:
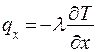 ,(13)
,(13)
т.е. плотность теплового потока пропорциональна коэффициенту теплопроводности и градиенту температуры. Знак “минус” указывает на то, что тепло передается от участка с большей температурой к участку с меньшей температурой. Равенство (13) называют законом теплопроводности Фурье.
Этот закон справедлив для точек, находящихся внутри тела. Все точки тела на его поверхности находятся в особых условиях, так как через поверхность тело взаимодействует с окружающей средой путем конвективного и лучистого теплообмена.
Для описания конвективного теплообмена используют закон теплообмена Ньютона
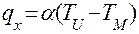 , (14)
, (14)
устанавливающий, что плотность теплового потока на поверхности тела пропорциональна коэффициенту теплообмена 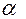 и разности температур нагрева
и разности температур нагрева  и поверхности металла
и поверхности металла 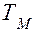 .
.
Лучистое излучение описывается законом Стефана-Больцмана, согласно которому плотность теплового потока излучения пропорциональна четвертой степени температуры тела:
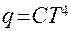 ,(15)
,(15)
где С – коэффициент, зависящий от состояния поверхности тела (степени черноты) и от температуры.
При температурах 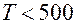 К основная часть теплоты приходится на долю конвективного теплообмена. В случае более высоких температур существенное значение приобретает лучистый теплообмен.
К основная часть теплоты приходится на долю конвективного теплообмена. В случае более высоких температур существенное значение приобретает лучистый теплообмен.
При определении температуры используют также уравнение теплопроводности, являющееся основным в области теплофизики. Оно устанавливает связь между температурой, координатами и временем применительно к твердому телу, когда тепло передается согласно закону Фурье. Его формулирование основано на законе сохранения энергии для элементарного объема внутри тела.
Уравнение теплопроводности для стержня малого сечения, когда тепло передается в одном направлении, имеет вид:
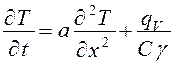 ,(16)
,(16)
где: 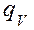 – удельная объемная мощность источника тепла внутри тела (например, тепло, выделяющееся благодаря прохождению электрического тока).
– удельная объемная мощность источника тепла внутри тела (например, тепло, выделяющееся благодаря прохождению электрического тока).
Если тепло передается по двум или трем направлениям, то уравнение теплопроводности соответственно будет иметь вид для пластины:
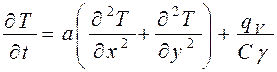 (17)
(17)
и для объемного тела:
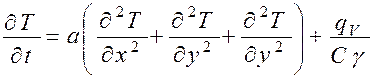 . (18)
. (18)
Если температура не изменяется во времени (установившееся температурное поле), то 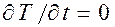 ; если отсутствует тепловыделение внутри металла, то
; если отсутствует тепловыделение внутри металла, то 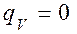 . В этих случаях уравнение теплопроводности упрощается.
. В этих случаях уравнение теплопроводности упрощается.
Уравнение теплопроводности имеет бесчисленное множество решений. Для решения конкретной задачи уравнение дополняется граничными и начальными условиями (условиями однозначности). Тогда задача будет иметь единственное решение. Реальные задачи расчета температуры применительно к процессам сварки отличаются высокой степенью сложности по следующим причинам:
1. Теплопроводность и теплоемкость материала 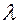 и
и 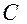 изменяются в значительных пределах, так как интервал температур очень широк (от 0 до
изменяются в значительных пределах, так как интервал температур очень широк (от 0 до 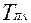 и выше), в связи с чем уравнение теплопроводности становится нелинейным.
и выше), в связи с чем уравнение теплопроводности становится нелинейным.
2. Граничные условия очень сложны в связи с тем, что по мере нагрева условия на поверхности сильно изменяются.
3. Задачи, как правило, двухмерны или трехмерны.
4. Имеются фазовые превращения, в результате которых свойства нагреваемого металла изменяются скачкообразно.
В связи с этим большинство задач решают с рядом упрощающих предположений, часто применяются численные методы с использованием ЭВМ.
Сложность таких задач не позволяет рассмотреть их в пределах данного курса. Ограничимся качественной оценкой температурных полей для различных случаев.
Дата добавления: 2015-07-18; просмотров: 2882;
