Дефект массы и энергия связи ядра
Исследования показывают, что атомные ядра являются устойчивыми образованиями. Это означает, что в ядре между нуклонами существует определенная связь. Изучение этой связи может быть проведено без привлечения сведений о характере и свойствах ядерных сил, а основываясь на законе сохранения энергии. Введём определения.
Энергией связи нуклона в ядре называется физическая величина, равная работе, которую необходимо совершить для удаления данного нуклона из ядра без сообщения ему кинетической энергии.
Полная энергия связи ядра определяется работой, которую нужно совершить для расщепления ядра на составляющие его нуклоны без придания им кинетической энергии.
Из закона сохранения энергии следует, что при образовании ядра из составляющих его нуклонов должна выделиться энергия, равная энергии связи ядра. Очевидно, что энергия связи ядра равна разности между суммарной энергией свободных нуклонов, составляющих данное ядро, и их энергией в ядре. Из теории относительности известно, что между энергией и массой имеется связь:
Е = mс2. (250)
Если через ΔЕсв обозначить энергию, выделяющуюся при образовании ядра, то с этим выделением энергии, согласно формуле (250), должно быть связано уменьшение суммарной массы ядра при его образовании из составных частиц:
Δm = ΔЕсв / с2 (251)
Если обозначить через mp, mn, mЯ соответственно массы протона, нейтрона и ядра, то Δm можно определить по формуле:
Dm = [Zmр + (A-Z)mn] - mЯ. (252)
Массу ядер очень точно можно определить с помощью масс-спектрометров - измерительных приборов, разделяющих с помощью электрических и магнитных полей пучки заряженных частиц (обычно ионов) с разными удельными зарядами q/m. Масс-спектрометрические измерения показали, что, действительно, масса ядра меньше, чем сумма масс составляющих его нуклонов.
Разность между сумой масс нуклонов, составляющих ядро, и массой ядра называется дефектом массы ядра (формула (252)).
Согласно формуле (251), энергия связи нуклонов в ядре определится выражением:
ΔЕСВ = [Zmp + (A-Z)mn – mЯ ]с2. (253)
В таблицах обычно приводятся не массы ядер mЯ, а массы атомов mа. Поэтому для энергии связи пользуются формулой
ΔЕСВ = [ZmH + (A-Z)mn – mа ]с2 (254)
где mH - масса атома водорода 1Н1. Так как mH больше mр, на величину массы электрона me, то первый член в квадратных скобках включает в себя массу Z электронов. Но, так как масса атома mа отличается от массы ядра mЯ как раз на массу Z электронов, то вычисления по формулам (253) и (254) приводят к одинаковым результатам.
Часто вместо энергии связи ядра рассматривают удельную энергию связиdЕСВ - это энергия связи, приходящаяся на один нуклон ядра. Она характеризует устойчивость (прочность) атомных ядер, т. е. чем больше dЕСВ,тем устойчивее ядро. Удельная энергия связи зависит от массового числа А элемента. Для легких ядер (А £ 12) удельная энергия связи круто возрастает до 6 ¸ 7 МэВ, претерпевая целый ряд скачков (см. рисунок 93). Например, для 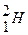 dЕСВ =1,1 МэВ, для
dЕСВ =1,1 МэВ, для 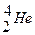 -7,1 МэВ, для
-7,1 МэВ, для 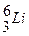 -5,3 МэВ. При дальнейшем увеличении массового числа dЕСВ возрастает более медленно до максимальной величины 8,7 МэВ у элементов с А=50¸60, а потом постепенно уменьшается для тяжелых элементов. Например, для
-5,3 МэВ. При дальнейшем увеличении массового числа dЕСВ возрастает более медленно до максимальной величины 8,7 МэВ у элементов с А=50¸60, а потом постепенно уменьшается для тяжелых элементов. Например, для 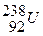 она составляет 7,6 МэВ. Отметим для сравнения, что энергия связи валентных электронов в атомах составляет примерно 10 эВ (в 106 раз меньше). На кривой зависимости удельной энергии связи от массового числа для стабильных ядер (рисунок 93) можно отметить следующие закономерности:
она составляет 7,6 МэВ. Отметим для сравнения, что энергия связи валентных электронов в атомах составляет примерно 10 эВ (в 106 раз меньше). На кривой зависимости удельной энергии связи от массового числа для стабильных ядер (рисунок 93) можно отметить следующие закономерности:
 а) Если отбросить самые легкие ядра, то в грубом, так сказать нулевом приближении, удельная энергия связи постоянна и равна примерно 8 МэВ на
а) Если отбросить самые легкие ядра, то в грубом, так сказать нулевом приближении, удельная энергия связи постоянна и равна примерно 8 МэВ на
нуклон. Приближенная независимость удельной энергии связи от числа нуклонов свидетельствует о свойстве насыщения ядерных сил. Это свойство состоит в том, что каждый нуклон может взаимодействовать только с несколькими соседними нуклонами.
б) Удельная энергия связи не строго постоянна, а имеет максимум (~8,7 МэВ/нуклон) при А = 56, т.е. в области ядер железа, и спадает к обоим краям. Максимум кривой соответствует наиболее стабильным ядрам. Легчайшим ядрам энергетически выгодно сливаться друг с другом с выделением термоядерной энергии. Для наиболее тяжелых ядер, наоборот, выгоден процесс деления на осколки, идущий с выделением энергии, получившей название атомной.
Наиболее устойчивыми оказываются так называемые магические ядра, у которых число протонов или число нейтронов равно одному из магических чисел: 2, 8, 20, 28, 50, 82, 126. Особенно стабильны дважды магические ядра, у которых магическими являются и число протонов, и число нейтронов. Этих ядер насчитывается всего пять: 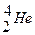 ,
, 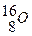 ,
, 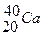 ,
, 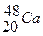 ,
, 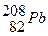 .
.
Дата добавления: 2015-07-18; просмотров: 1843;
