Надежность единичного элемента

Нам уже известно, что под надежностью элемента или системы понимается их свойство выполнять свои функции в течение заданного промежутка времени или заданной наработки.

Существует много причин, обусловливающих недостаточную надежность элементов и систем.

Первую группу составляют ошибки, допущенные при конструировании, определении условий эксплуатации, изготовлении и монтаже оборудования. Эти ошибки выражаются в повышенной частоте отказов, особенно при освоении и запуске в изготовление новых изделий.

Другая группа факторов приводит к постепенному утрачиванию элементом или системой своих первоначальных свойств. Это явление выражается в основном различными видами старения. Однако результат этих закономерных изменений может проявиться внезапно, т.е. имеет случайный характер.

Третья группа — это непредвиденные, непредсказуемые воздействия на элемент или систему, чаще всего физического характера, называемые стрессами. Эти воздействия приводят к катастрофическим или мгновенным отказам.

Эти три группы вызывают необратимое изменение свойств элементов и систем — система приходит в негодность частичную или полную.

Существуют воздействия, которые вызывают временный отказ, действие которого исчезает после исчезновения причин, вызвавших отказ. Такие временные или самоустраняющиеся отказы именуются сбоями. Например, сбой может появиться в электронной системе в результате помех (например, в телевизоре). Резюмируя все вышеизложенное, можно отметить, что во всех случаях отказ элемента системы является случайным событием и поэтому может описываться аппаратом теории вероятностей.

Следует указать, что получение достаточно достоверных математических выводов возможно при весьма большом объеме информации об отказах, и в этом главный недостаток этого метода.

Для различных элементов и систем решающую роль имеют различные показатели надежности, т. к. нас интересуют весьма разные показатели работы в разных случаях. Элемент или система может иметь множество состояний, различающихся между собой с точки зрения надежности. Для описания связи конкретных элементов множества и связи этих элементов между собой нужно разработать математическую модель, описывающую это множество.

Общий подход к построению моделей надежности заключается в следующем.

В качестве первого шага построения математической модели необходимо выбрать соответствующее фазовое пространство системы или элемента 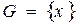("Множество G содержит x элементов").

С течением времени в составных частях системы происходят различные изменения, например старение. Поэтому, если в момент времени t₁состояние системы описывалось точкой х₁ , то в момент t₂состояние системы описывается точкой x₂. При этом может оказаться, что x₁¹ x₂. Если обозначить через х(t) Î (:x функция от t принадлежит множеству G) состояние системы в момент времени t, то последовательность состояний х(t), где t³0 можно рассматривать, как процесс, протекающий во времени. Т.к. изменения зависят от случайных причин, то х(t) можно рассматривать как траекторию случайного процесса, протекающего в фазовом пространстве G.

Вторым шагом построения математической модели является определение этого случайного процесса в зависимости от конкретных условий задачи. То есть необходимо найти математическую закономерность эволюции процесса.

Третий шаг заключается в выборе различных числовых характеристик надежности системы. Такой выбор зависит от конкретных условий и назначения системы. В самом общем плане характеристики надежности можно рассматривать как математическое ожидание от некоторого функционала Ф, определенного на траекториях х (t) (Функционалом в рассматриваемом случае является некоторое числовое значение, характеризующее значение функции на траектории, лежащей в пространстве устойчивой работы системы или элемента).

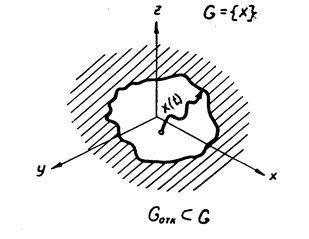
Рис. 3.1. Схематическая модель фазового пространства и траектории случайного процесса.

Функционал Ф определен на процессе х(t), если каждой траектории х(t) ставится в соответствие некоторое число Ф[х(t)]. Показатель надежности j определяется как математическое ожидание от этого функционала, т.е.

j =МФ[х(t)]. (3.1)

Такой подход фактически состоит в том, что каждой траектории процесса мы приписываем некоторый вес (значимость), а затем за показатель надежности принимаем среднее значение этого веса (рис. 3.1).

Задано фазовое пространство G = {х}. В нем определено подмножество G_откÌG, в котором система будет считаться неработоспособной, т. к. ее состояние х(t) Î G.

Отказ системы наступит тогда, когда траектория х(t)достигнет границы подмножества G_отк и войдет в него.

Количественный показатель надежности системы в каждой точке траектории будет определяться некоторым числовым значением, определяемым по формуле (3.1).

Такова в общем виде методика подхода к определению характеристик надежности.