ОСНОВЫ ТЕОРИИ КОДИРОВАНИЯ
3.1. Назначение и классификация кодов
В этой главе будет рассматриваться кодирование дискретных сообщений, передаваемых в дискретном канале, т.е. кодирование в узком смысле. Следует напомнить. Что кодированием в широком смысле называют любое преобразование сообщения в сигнал путем установления взаимного соответствия.
Пусть источник выдает некоторое дискретное сообщение А, которое можно рассматривать как последовательность элементарных сообщений или символов аi (i = 1, 2, . . . К). Совокупность символов аi называется алфавитом источника, а К - объемом алфавита.
Кодирование заключается в том, что каждый символ источника (сообщения) аi заменяется последовательностью кодовых символов - кодовой комбинацией. Совокупность правил, по которым образуется набор кодовых комбинаций, однозначно соответствующий алфавиту источника, называется кодом.
При кодировании отдельным символам аi удобно сопоставить целые числа от 0 до К-1, обозначив их, например, Mi
Любое число M может быть представлено в позиционной системе счисления с основанием m в виде
M = bn-1mn-1 + bn-2mn-2 +. . . + b1m1 + b0m0(3.1)
Основанием позиционной системы счисления называется количество символов в алфавите системы счисления, а в качестве коэффициентов bi в (3.1) могут использоваться только символы, входящие в алфавит этой системы, т.е. bi могут принимать значения 0, 1, . . . , m-1.
Тогда кодирующее преобразование можно отобразить так
аi ® Mi ® (bn-1 bn-2 . . . b1 b0),(3.2)
где выражение в скобках представляет собой совокупность коэффициентов полинома (3.1), называемую кодовой комбинацией для аi. Такое преобразование является взаимно однозначным и обратимым, если не учитывать воздействия помех, что позволяет осуществлять декодирование.
Число m символов в алфавите кода называется основанием кода.
Число разрядов n в каждой кодовой комбинации постоянно при всех i, т.е. n=const, то такой код называется равномерным.
Необходимость замены каждого символа аi из К символов источника последовательностью кодовых символов (bn-1 bn-2 . . . b1 b0) или кодовой комбинацией объясняется тем, что в большинстве случаев объем алфавита K>m, т.е. основания кода или объема алфавита кодовых символов. Например, в телеграфном коде каждая буква русского алфавита (К=32) кодируется кодовой комбинацией из n=5 двоичных (m=2) символов (0 и 1).
Если сообщение «а» заменяется кодовой комбинацией «b» при условии их однозначного соответствия и обратимости преобразования, то на основе свойств взаимной информации (2.13. и 2.14) можно записать I(a,b) = H(a) = =H(b), где I(a,b) - количество информации в кодовой последовательности «b» относительно сообщения «а», H(a) - энтропия сообщения, H(b) - энтропия кодовой последовательности. Следовательно, при кодировании энтропия не меняется.
Иначе обстоит дело с избыточностью, определяемой соотношением между энтропией (2.5) и ее максимальным значением при данном объеме алфавита (2.4). Поскольку при кодировании чаще всего происходит изменение объемов алфавитов, избыточность может как возрастать, так и уменьшаться.
Число возможных кодовых комбинаций из n разрядов для кода с основанием m равно N=mn . Если из этих N комбинаций для кодирования используется только часть, равная Nр, которые называются рабочими или разрешенными, то величина Nр называется мощностью кода.
Избыточность кода характеризуется коэффициентом избыточности
rк = 1 - (logmNp / logmN). (3.3)
Код, у которого Nр = N , т.е. используются все возможные комбинации, имеет rк = 0 и называется безизбыточным или неизбыточным.
Простейшим безизбыточным равномерным кодом является обычный двоичный (m=2) n-разрядный код, называемый иногда кодом на все сочетания. Число комбинаций такого кода N = 2n.
К таким кодам можно отнести уже упомянутый телеграфный код, а также стандартные коды для обмена информацией КОИ-7, КОИ-8, ASCII и другие.
Еще одним примером простейшего двоичного кода на все сочетания является код, называемый отраженным или рефлексным кодом, у которого каждая кодовая комбинация отличается от соседней содержимым лишь одного разряда. Наибольшее распространение из таких кодов получил код Грея, основным преимуществом которого по сравнению с другими рефлексными кодами является простота преобразования из обычного двоичного кода в код Грея и обратно. Обычный двоичный код преобразуется в код Грея путем суммирования по модулю 2 данной комбинации двоичного кода и такой же точно комбинации, но сдвинутой на один разряд вправо с отбрасыванием младшего (правого) разряда.
Например: 1101
Или, другими словами, если начинать преобразование с младшего (правого) разряда, то алгоритм выглядит следующим образом: «Если последующий разряд равен 1, то данный разряд инвертируется, если последующий разряд равен 0, то данный разряд остается неизменным. Старший разряд остается неизменным».
Пример 3.1. Составить таблицу соответствия обычного двоичного четырехразрядного кода и кода Грея.
Решение. Таблица соответствия обычного двоичного четырехразрядного кода и кода Грея будет выглядеть следующим образом.
| Десятичный эквивалент | Обычный двоичный код | Код Грея |
Функциональная схема преобразователя обычного двоичного кода в код Грея для четырехразрядных комбинаций представлена на рис. 3.1
 Рис. 3.1
Рис. 3.1
|
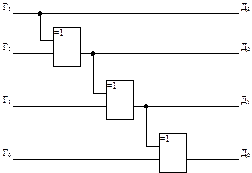 Рис. 3.2
Рис. 3.2
|
Обратное преобразование из кода Грея в обычный двоичный код осуществляется в соответствии со следующим алгоритмом: 1. Старший разряд кодовой комбинации кода Грея остается без изменений. 2. Каждый последующий разряд, начиная от старшего, инвертируется столько раз, сколько единиц ему предшествует в кодовой комбинации кода Грея.
Пример 3.2. Синтезировать функциональную схему четырехразрядного преобразователя кода Грея в обычный двоичный код.
Решение. Функциональная схема четырехразрядного преобразователя кода Грея в обычный двоичный код представлена на рис. 3.2
Преимущества кода Грея проявляются при преобразованиях аналоговых (непрерывных) величин в код. Если при таком преобразовании используется обычный двоичный код, то некоторые комбинации отличаются друг от друга во всех разрядах и при считывании такого кода может возникнуть ошибка, достигающая максимальной величины 2n-1, где n - число разрядов кода. Например, комбинация 0111 при неправильном считывании старшего разряда преобразуется в комбинацию 1111, т.е. ошибка составит величину 15-7 =8 = 24-1. При тех же значениях и при той же ошибке, но при использовании кода Грея (см. таблицу) комбинация 0100 будет считана как 1100, т.е. ошибка составит величину 8-7, т.е. единицу младшего разряда.
Еще одним классом примитивных кодов, используемых при различных промежуточных преобразованиях, являются т.н. двоично-десятичные коды. В таком коде каждая цифра (декада) десятичного числа записывается в виде четырехразрядного двоичного числа (тетрады). С помощью 4 разрядов можно образовать 24 = 16 различных комбинаций, из которых любые 10 могут составить алфавит двоично-десятичного кода. В связи с этим существует большое количество различных двоично-десятичных кодов. Наиболее употребительные из них представлены в таблице.
| Десятичная цифра | Код 8421 | Код 5421 | Код 2421 | Код «с избытком 3» |
Двоично-десятичные коды, в отличие от рассмотренных ранее, обладают некоторой избыточностью 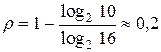 , но это их свойство практически не используется для обнаружения ошибок.
, но это их свойство практически не используется для обнаружения ошибок.
Отметим в связи с этим общее негативное свойство безизбыточных кодов. При передаче кодовой комбинации безизбыточного кода по каналу связи в ней под воздействием помех возникают ошибки, но никаких признаков ошибочности принятая комбинация иметь не будет, поскольку вследствие безизбыточности любая подвергшаяся воздействию помех комбинация преобразуется в другую разрешенную или рабочую комбинацию.
Рассмотренные до сих пор безизбыточные коды были равномерными, т.е. содержали одинаковое число разрядов в каждой кодовой комбинации вне зависимости от статистических свойств символов источника, кодируемых этими комбинациями. В том случае, если символы источника неравновероятны, такие коды окажутся избыточными. Уменьшение существующей избыточности источника является задачей т.н. эффективного кодирования или кодирования для источника. Алгоритмы построения наиболее известных эффективных кодов будут рассмотрены в разделе 3.2. Здесь же отметим, что вследствие упомянутого выше негативного свойства безизбыточных кодов эффективное кодирование в чистом виде используется только тогда, когда кодовые комбинации не подвергаются воздействию помех.
Если при кодировании не устранять, а специальным образом вводить избыточность, то это приводит к увеличению возможностей по обнаружению и даже исправлению ошибок в принятых кодовых комбинациях. Такое кодирование называют помехоустойчивым или кодированием для канала. При помехоустойчивом кодировании чаще всего считают избыточность источника равной или близкой к нулю. Если это не так, то целесообразно уменьшить избыточность источника методами эффективного кодирования, а затем методами помехоустойчивого кодирования ввести такую избыточность, которая позволит увеличить верность передачи. Классификация и алгоритмы построения основных классов помехоустойчивых кодов будут рассмотрены в последующих разделах настоящей главы.
3.2. Эффективное кодирование
Целью эффективного кодирования является устранение избыточности сообщений, поскольку избыточные сообщения требуют большего времени для передачи и большего объема памяти для хранения.
Очевидно, что для уменьшения избыточности кодовых комбинаций, кодирующих символы сообщений, необходимо выбирать максимально короткие кодовые комбинации. Однако для полного устранения избыточности этого недостаточно. При кодировании необходимо учитывать вероятности появления каждого символа в сообщениях и наиболее вероятным символам сопоставлять короткие кодовые комбинации, а наименее вероятным - более длинные.
В качестве иллюстрации - простой пример. Пусть сообщение может состоять из двух слов. Длина первого - один кодовый символ, второго - три кодовых символа. Вероятности появления слов в сообщении соответственно 0,1 и 0,9. Тогда статистически средняя длина слова в сообщении 1*0,1 + 3*0,9 = 2,8 символа. Если слова будут иметь другие вероятности, например, 0,9 и 0,1, то средняя длина слова составит 1*0,9 + 3*0,1 = 1,2 символа. Отсюда видно, что длина кодовой комбинации должна выбираться в зависимости от вероятности появления кодируемого этой комбинацией символа сообщения. Чем чаще он появляется, т.е. чем больше его вероятность, тем более короткую кодовую комбинацию ему следует сопоставить.
Формализуем задачу эффективного кодирования. Пусть входным алфавитом кодирующего отображения является множество сообщений 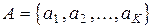 . Пусть выходным алфавитом кодирующего отображения будет множество В , число элементов которого равно m .Кодирующее отображение сопоставляет каждому сообщению аi кодовую комбинацию, составленную из ni символов алфавита В . Требуется оценить минимальную среднюю длину кодовой комбинации. Сравнивая ее со средней длиной кодовой комбинации, вычисленной для какого-либо конкретного кода, можно оценить, насколько данный конкретный код находится близко к эффективному, т.е. безизбыточному коду.
. Пусть выходным алфавитом кодирующего отображения будет множество В , число элементов которого равно m .Кодирующее отображение сопоставляет каждому сообщению аi кодовую комбинацию, составленную из ni символов алфавита В . Требуется оценить минимальную среднюю длину кодовой комбинации. Сравнивая ее со средней длиной кодовой комбинации, вычисленной для какого-либо конкретного кода, можно оценить, насколько данный конкретный код находится близко к эффективному, т.е. безизбыточному коду.
Энтропия сообщения А по определению (2.3)
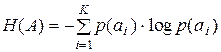 . (3.4)
. (3.4)
Средняя длина кодовой комбинации
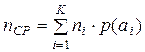 , (3.5)
, (3.5)
где ni - длина кодовой комбинации, сопоставленной сообщению аi. Максимальная энтропия, которую может иметь сообщение из nСР символов алфавита В, число элементов которого равно m , равна в соответствии с (2.4)
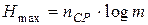 . (3.6)
. (3.6)
Очевидно, что для обеспечения передачи информации, содержащейся в сообщении А, с помощью кодовых комбинаций алфавита В должно выполняться неравенство
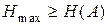 (3.7)
(3.7)
или с учетом (3.6) 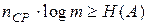 или с учетом (3.4)
или с учетом (3.4)
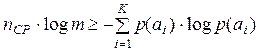 . (3.8)
. (3.8)
При строгом неравенстве (3.7) закодированное сообщение обладает избыточностью, т.е. для кодирования используется больше символов, чем это минимально необходимо. Для числовой оценки избыточности в предыдущей главе использовался коэффициент избыточности
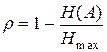 . (3.9)
. (3.9)
Поскольку из (3.6) и (3.7) следует, что 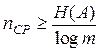 , то ясно, что
, то ясно, что
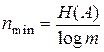 . (3.10)
. (3.10)
Тогда формулу (3.9) для коэффициента избыточности для кода можно переписать в следующем виде
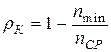 . (3.11)
. (3.11)
Под эффективным кодом понимается код, rК которого равен 0, т.е. для абсолютно эффективных кодов 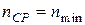 . Тогда и неравенство (3.8) переходит в равенство
. Тогда и неравенство (3.8) переходит в равенство 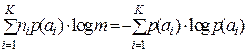 , откуда
, откуда 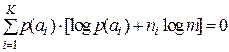 .
.
Предположив очевидное, что А не содержит элементов с p(ai) = 0, получим
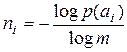 (3.12)
(3.12)
для всех i. Но отношение (3.12) не всегда дает целочисленный результат. Следовательно, не для любого набора А с заданным распределением вероятностей p(ai) можно построить абсолютно эффективный код с rК = 0. Тем не менее, всегда можно обеспечить выполнение неравенства 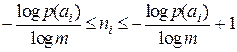 , умножая которое на p(ai) и суммируя по i , получим
, умножая которое на p(ai) и суммируя по i , получим
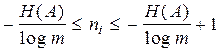 . (3.13)
. (3.13)
Неравенство (3.13) может служить критерием для оценки эффективности какого-либо конкретного кода.
Для построения эффективных кодов используются различные алгоритмы. Одним из них является код Шеннона - Фано. Код Шеннона - Фано строится следующим образом. Символы алфавита источника выписываются в порядке убывания их вероятностей. Затем вся совокупность разделяется на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковыми. Далее всем символам одной группы в качестве первого кодового символа приписывается 1, а другой группы - 0. Далее каждая из полученных групп в свою очередь разбивается на две подгруппы с одинаковыми суммарными вероятностями и т.д. Процесс повторяется до тех пор, пока в каждой группе останется по одному символу.
Пример 3.3. Закодировать двоичным кодом Шеннона - Фано ансамбль {ai} (i=1,2,...,8), если вероятности символов ai имеют следующие значения
| ai | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| pi | 0,25 | 0,25 | 0,125 | 0,125 | 0,0625 | 0,0625 | 0,0625 | 0,0625 |
Найти среднее число символов в кодовой комбинации и коэффициент избыточности кода.
Решение.
| ai | pi | кодовая комбинация | ni | pini | H(ai) |
| a1 | 0,25 | 11 | 2 | 0,5 | 0,5 |
| a2 | 0,25 | 10 | 2 | 0,5 | 0,5 |
| a3 | 0,125 | 011 | 3 | 0,375 | 0,375 |
| a4 | 0,125 | 010 | 3 | 0,375 | 0,375 |
| a5 | 0,0625 | 0011 | 4 | 0,25 | 0,25 |
| a6 | 0,0625 | 0010 | 4 | 0,25 | 0,25 |
| a7 | 0,0625 | 0001 | 4 | 0,25 | 0,25 |
| a8 | 0,0625 | 0000 | 4 | 0,25 | 0,25 |
По формуле (3.5) 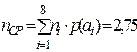 , по формуле (3.4)
, по формуле (3.4) 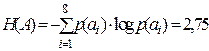 , тогда по формуле (3.10)
, тогда по формуле (3.10) 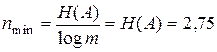 и по формуле (3.11)
и по формуле (3.11) 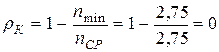 , таким образом, построен абсолютно эффективный код.
, таким образом, построен абсолютно эффективный код.
Алгоритм кодирования Шеннона - Фано имеет простую графическую иллюстрацию в виде графа, называемого кодовым деревом. Граф для кода Шеннона - Фано строится следующим образом. Из нижней или корневой вершины графа исходят два ребра, одно из которых помечается символом 0, а другое – 1. Эти два ребра соответствуют разбиению множества символов алфавита источника на две примерно равновероятные группы, одной из которых сопоставляется кодовый символ 0, а другой – 1. Ребра, исходящие из вершин следующего уровня, соответствуют разбиению получившихся групп на равновероятные подгруппы и т.д. Построение графа заканчивается, когда множество символов алфавита источника будет разбито на одноэлементные подмножества. Каждая концевая вершина графа, т.е. вершина, из которой уже не исходят ребра, соответствует некоторой кодовой комбинации. Чтобы сформировать эту комбинацию, надо пройти путь от корневой вершины до соответствующей концевой, выписывая в порядке следования по этому пути кодовые символы с ребер пути.
Рассмотренная методика Шеннона - Фано не всегда приводит к однозначному построению кода, поскольку в зависимости от вероятностей отдельных символов можно несколькими способами осуществить разбиение на группы.
Пример 3.4. Закодировать двоичным кодом Шеннона - Фано ансамбль {ai} (i=1,2,...,8), если вероятности символов ai имеют следующие значения
| ai | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| pi | 0,22 | 0,20 | 0,16 | 0,16 | 0,10 | 0,10 | 0,04 | 0,02 |
Найти коэффициент избыточности кода.
Дата добавления: 2015-07-14; просмотров: 1784;
