Решение.2
| ai | pi | кодовая комбинация | ni | pini | H(ai) |
| a1 | 0,22 | 11 | 2 | 0,44 | 0,4806 |
| a2 | 0,20 | 10 | 2 | 0,40 | 0,4643 |
| a3 | 0,16 | 011 | 3 | 0,48 | 0,4230 |
| a4 | 0,16 | 010 | 3 | 0,48 | 0,4230 |
| a5 | 0,10 | 001 | 3 | 0,30 | 0,3322 |
| a6 | 0,10 | 0001 | 4 | 0,40 | 0,3322 |
| a7 | 0,04 | 00001 | 5 | 0,20 | 0,1857 |
| a8 | 0,02 | 00000 | 5 | 0,10 | 0,1129 |
По формуле (3.5) 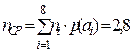 , по формуле (3.4)
, по формуле (3.4) 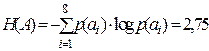 , тогда по формуле (3.10)
, тогда по формуле (3.10) 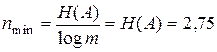 и по формуле (3.11)
и по формуле (3.11) 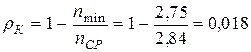 , т.е. второй вариант решения ближе к оптимальному, поскольку обеспечивает меньший коэффициент избыточности.
, т.е. второй вариант решения ближе к оптимальному, поскольку обеспечивает меньший коэффициент избыточности.
От данной неоднозначности построения эффективного кода свободен код Хаффмена. Для двоичного кода методика Хаффмена сводится к следующему. Символы алфавита источника выписываются в основной столбец таблицы в порядке убывания вероятностей. Далее два последних символа объединяются в один вспомогательный с вероятностью, равной сумме вероятностей объединяемых символов. Вероятности символов, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания в дополнительном столбце таблицы, после чего два последних символа вновь объединяются. Процесс повторяется до тех пор, пока не буде получен единственный вспомогательный символ с вероятностью, равной 1. Для составления кодовых комбинаций, соответствующих символам, необходимо проследить пути переходов по строкам и столбцам таблицы.
Для наглядного представления этого процесса удобнее всего построить граф, называемый кодовым деревом. Процедура построения кодового дерева выглядит следующим образом. Из вершины, соответствующей последнему единственному вспомогательному символу с вероятностью, равной 1, направляются две ветви, причем ветви с большей вероятностью присваивается кодовый символ 1, а с меньшей - 0. Такое последовательное ветвление из вершин, соответствующих вспомогательным символам, продолжается до получения вершин, соответствующих основным исходным символам.
Пример 3.5. Закодировать двоичным кодом Хаффмена ансамбль из примера 3.4. Решение представлено на рис. 3.3.
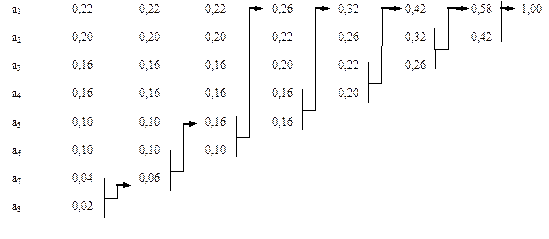
Рис. 3.3
Кодовое дерево для этого примера изображено на рис. 3.4
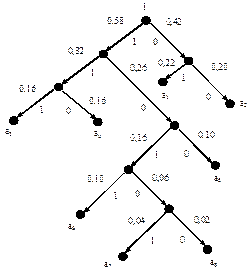 Рис. 3.4
Рис. 3.4
| Составленная в соответствии с графом таблица кодовых комбинаций
|
Таким образом, получены те же параметры в смысле избыточности, что и в примере 3.4, решение 2 для кода Шеннона - Фано, хотя кодовые комбинации по составу другие.
Из рассмотрения методов построения эффективных кодов следует, что эффект уменьшения избыточности достигается за счет различия в числе разрядов в кодовых комбинациях, т.е. эти эффективные коды являются неравномерными, а это приводит к дополнительным трудностям при декодировании. Как вариант, можно для различения кодовых комбинаций ставить специальный разделительный символ, но при этом снижается эффект, т.к. средняя длина кодовой комбинации увеличивается на один разряд.
Более целесообразно обеспечить однозначное декодирование без введения дополнительных разрядов. Для этого эффективный код необходимо строить так, чтобы ни одна комбинация кода не совпадала с началом другой более длинной кодовой комбинации. Коды, удовлетворяющие этому условию, называются префиксными.
Наличие или отсутствие свойства префиксности отражается и на кодовом дереве. Если свойство префиксности отсутствует, то некоторые промежуточные вершины кодового дерева могут соответствовать кодовым комбинациям.
Префиксные коды иногда называют мгновенно декодируемыми, поскольку конец кодовой комбинации опознается сразу, как только мы достигаем конечного символа кодовой комбинации при чтении кодовой последовательности. В этом состоит преимущество префиксных кодов перед другими однозначно декодируемыми неравномерными кодами, для которых конец каждой кодовой комбинации может быть найден лишь после анализа одной или нескольких последующих комбинаций, а иногда и всей последовательности. Это приводит к тому, что декодирование осуществляется с запаздыванием по отношению к приему последовательности.
Очевидно, что практическое применение могут иметь только префиксные коды. Коды Шеннона - Фэно и Хаффмена являются префиксными.
При использовании префиксных кодов возникает вопрос о том, каковы возможные длины кодовых комбинаций префиксного кода. Пусть a1, a2, . . . , aN - кодовые комбинации префиксного двоичного кода. Пусть nk -число кодовых комбинаций длины k . Число nk совпадает с числом вершин k-го уровня кодового дерева. Конечно справедливо неравенство nk £ 2k, поскольку 2k - максимально возможное число вершин на k-м уровне двоичного дерева. Однако для префиксного кода можно получить гораздо более точную оценку. Если n1, n2, . . . , nk-1 - число вершин 1-го, 2-го, . . . , (k-1)-го уровней дерева, то число всех вершин k-го уровня кодового дерева префиксного кода равно 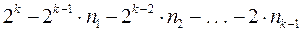 , и поэтому
, и поэтому 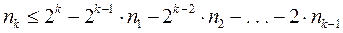 , или иначе
, или иначе 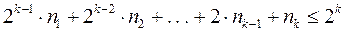 .
.
Деля обе части неравенства на 2k,получим 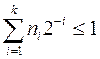 . Это неравенство справедливо для любого k£L , где L - максимальная длина кодовых комбинаций
. Это неравенство справедливо для любого k£L , где L - максимальная длина кодовых комбинаций 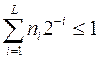 . Если обозначить l1, l2, . . . , lN длины кодовых комбинаций a1, a2, . . . , aN , то последнее неравенство можно записать следующим образом
. Если обозначить l1, l2, . . . , lN длины кодовых комбинаций a1, a2, . . . , aN , то последнее неравенство можно записать следующим образом 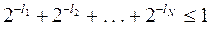 .
.
Это и есть условие, которому должны удовлетворять длины кодовых комбинаций двоичного префиксного кода. Это неравенство в теории кодирования называется неравенством Крафта и является достаточным условием того, что существует префиксный код с длинами кодовых комбинаций l1, l2, . . . , lN .
Если кодовый алфавит содержит не два, а S символов, то подобным же образом доказывается, что необходимым и достаточным условием для существования префиксного кода является выполнение неравенства 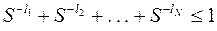 .
.
Дата добавления: 2015-07-14; просмотров: 658;
