ПОНЯТИЕ О ИСПЫТАНИИ И КОНТРОЛЕ

Испытанием называется экспериментальное определение количественных и (или) качественных характеристик свойств объекта испытаний как результата воздействия на него, при его функционировании, при моделировании объекта и (или) воздействий. Экспериментальное определение характеристик свойств объекта при испытаниях может проводиться путем измерений, оценивания и контроля. Объектом испытаний является продукция или процессы ее производства и функционирования.

Важнейшими признаками любых испытаний являются:

•принятие на основе их результатов определенных решений по объекту испытаний, например о его годности, или браковке, о возможности предъявления на следующие испытания и т.д.;

•задание требуемых реальных или моделируемых условий испытаний.

Под условиями испытаний понимается совокупность воздействующих факторов и (или) режимов функционирования объекта при испытаниях. В нормативных документах на испытания конкретных объектов должны быть определены нормальные условия испытаний.

Целью испытаний следует считать нахождение истинного значения параметра или характеристики не при тех реальных условиях, в которых он фактически может находится в ходе испытаний, а' в заданных номинальных условиях испытания. Реальные условия испытаний практически всегда отличаются от номинальных, поскольку установить параметры условий испытаний абсолютно точно невозможно. Следовательно, результат испытания всегда имеет погрешность, возникающую не только вследствие неточного определения искомой характеристики, но и из-за неточного установления номинальных условий испытания.

Результатом испытаний называется оценка характеристик свойств объекта, установления соответствия объекта заданным требованиям по данным испытаний, результаты анализа качества функционирования объекта в процессе испытаний. Результат испытаний характеризуется точностью – свойством испытаний, показывающим близость их результатов к действительным значениям характеристик объекта в определенных условиях испытаний.

Между измерением и испытанием существует большое сходство:

•результаты обеих операций выражаются в виде чисел;

•погрешности обеих операций могут быть выражены как разности между результатом измерения (испытания) и истинным значением измеряемой величины (или определяемой характеристики при номинальных условиях эксплуатации).

Однако с точки зрения метрологии между ними имеется значительное отличие: погрешность измерения является только одной из составляющих погрешности испытания. Поэтому можно сказать, что испытание – это более общая операция, чем измерение. Измерение можно считать частным случаем испытания, при котором условия испытаний не представляют интереса.

Контролем называется процесс определения соответствия значения параметра изделия установленным требованиям или нормам. Сущность всякого контроля состоит в проведении двух основных этапов. На первом из них проводится получение информации о фактическом состоянии некоторого объекта, о признаках и показателях его свойств. Эта информация называется первичной. На втором этапе первичная информация сопоставляется с заранее установленными требованиями, нормами, критериями. При этом выявляются соответствия или несоответствия фактических данных требуемым. Информация о расхождении фактических и требуемых данных называется вторичной. Вторичная информация используется для выработки соответствующих решений по поводу объекта контроля. В ряде случаев граница между этапами контроля неразличима, первый этап может быть выражен нечетко или практически не наблюдаться. Характерным примером такого рода является контроль размера детали калибром, сводящийся к операции сопоставления фактического и предельно допустимого значений параметра.

Контроль состоит из ряда элементарных операций: измерительного преобразования контролируемой величины; воспроизведения установок контроля; сравнения и получения результата контроля.

Измерения и контроль тесно связаны друг с другом, близки по своей информационной сущности и содержат ряд общих операций (например, сравнение, измерительное преобразование). В то же время процедуры измерения и контроля во многом различаются:

•результатом измерения является количественная характеристика, а контроля – качественная;

•измерение осуществляется в широком диапазоне значений измеряемой величины, а контроль – обычно в пределах небольшого числа возможных состояний;

•контрольные приборы, в отличие от измерительных, применяются для проверки состояния изделий, параметры которых заданы и изменяются в узких пределах;

•основной характеристикой качества процедуры измерения является точность, а процедуры контроля – достоверность.

В практике большое распространение получил так называемый допусковый контроль [37], суть которого состоит в определении путем измерения или испытания значения контролируемого параметра объекта и сравнения полученного результата с заданными граничными допустимыми значениями. Частным случаем допускового контроля является поверка средств измерений, в процессе которой исследуется попадание погрешностей СИ в допускаемые пределы.

При допусковом контроле возможны три зоны контролируемого состояния:

•ниже допускаемого значения (Х<ХН);

•выше допускаемого значения (Х>ХВ);

•между верхним и нижним допускаемыми значениями (Х_Н< Х< ХВ).

Результатом контроля является не число, а одно из взаимоисключающих утверждений:

•контролируемая характеристика (параметр) находится в пределах допускаемых значений, т.е, результат контроля – «годен»,

контролируемая характеристика (параметр) находится за пределами допускаемых значений, т.е. результат контроля – «не годен» или «брак».

Для определенности примем, что решение «годен» должно приниматься, если выполняется условие Х_Н£ Х £ Х_В,, где Х, Х_В,Х_Н– истинное значение и допускаемые верхнее и нижнее значения контролируемого параметра соответственно. На самом же деле с допускаемыми значениями Х_В и Х_Н сравнивается не истинное значение Х (поскольку оно неизвестно), а его оценка Х_0, полученная в результате измерений. Значение Х₀ , отличается от Х на величину погрешности измерения: Х=Х₀ + ∆ .Таким образом, решение «годен» при проведении контроля принимается в случае выполнения неравенства ХН≤ Х 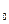≤Х_{В .}

Отсюда следует, что при допусковом контроле возможны четыре исхода.

1. Принято решение «годен», когда контролируемый параметр находится в пределах допускаемых значений, т.е. имели место события Х_Н≤Х≤Х_В и Х_Н≤Х₀≤Х_В. Если известны плотности вероятностей законов распределения F(х) контролируемого параметра х и погрешности его измерения F(∆), то при взаимной независимости этих законов и заданных допустимых верхнем и нижнем значениях параметра вероятность события «годен».

2. Принято решение «брак», когда контролируемый параметр находится вне пределов допускаемых значений, т. е. имели место события Х<ХН или Х > ХВ либо в Х₀< ХН или Х₀>ХВ. При оговоренных допущениях вероятность события «негоден» или «брак»

3. Принято решение «брак», когда истинное значение контролируемого параметра находится в пределах допускаемых значений, т.е. имели место события Х₀<ХН или Х₀ >ХВ и ХН≤ Х≤ХВ , и забракован исправный объект. В этом случае принято говорить, что существует ошибка первого рода. Ее вероятность

4. Принято решение «годен», когда истинное значение контролируемого параметра лежит вне пределов допускаемых значений, т.е. имели место события Х<ХН или Х>ХВ и ХН≤Х0≤ХВ, и неисправный объект признан годным. В этом случае говорят, что имеется ошибка второго рода, вероятность которой

Очевидно, что ошибки первого и второго родов имеют разное значение для изготовителей и потребителей (заказчиков) контролируемой продукции. Ошибки первого рода приводят к прямым потерям изготовителя, так как ошибочное признание негодным в действительности годного изделия приводит к дополнительным затратам на исследование, доработку и регулировку изделия. Ошибки второго рода непосредственно сказываются на потребителе, который получает некачественное изделие. При нормальной организации отношений между потребителем и производителем брак, обнаруженный первым из них, приводит к рекламациям и ущербу для изготовителя.

Рассмотренные вероятности РГ, РНГ, Р₁ и Р₂ при массовом контроле партии изделий характеризуют средние доли годных, негодных, неправильно забракованных и неправильно пропущенных изделий среди всей их контролируемой совокупности. Очевидно, что

РГ + РНГ+ Р₁+ Р₂= 1.

Достоверность результатов допускового контроля описывается различными показателями, среди которых наибольшее распространение получили вероятности ошибок первого Р1 и второго Р2, родов и риски изготовителя и заказчика (потребителя)

Rизг =P₁/(P₂+РНГ ); RЗАК=P₂/(P₂+P_r).

Одной из важнейших задач планирования контроля является выбор оптимальной точности измерения контролируемых параметров. При завышении допускаемых погрешностей измерения уменьшается стоимость средств измерений, но повышаются вероятности ошибок при контроле, что в конечном итоге приводит к потерям. При занижении допускаемых погрешностей стоимость СИ увеличивается (уменьшая вероятность ошибок контроля), что приводит к росту себестоимости выпускаемой продукции. Очевидно, что существует некоторая оптимальная точность, соответствующая минимуму суммы потерь от брака и стоимости контроля.

Приведенные формулы позволяют осуществить целенаправленный поиск таких значений погрешности измерения, которые при заданных значениях верхнего и нижнего значений контролируемого параметра обеспечили бы допускаемые значения и вероятностей ошибок первого Р_1д и второго Р_2д родов или соответствуюших рисков. Этот поиск проводится путем численного или графического интегрирования. Следовательно, для рационального выбора точностных характеристик СИ, используемых при проведении контроля, в каждом конкретном случае должны быть заданы допускаемые значения вероятностей Р_1д и Р_2д.

3 ТЕОРИЯ ВОСПРОИЗВЕДЕНИЯ ЕДИНИЦ ФИЗИЧЕСКИХ

ВЕЛИЧИН И ПЕРЕДАЧЕ ИХ РАЗМЕРОВ

3.1 СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН И ИХ ЕДИНИЦ

Описание свойств окружающих нас физических объ­ектов производится посредством ФВ, каждая из которых является качественно общей для многих объектов, но в количественном отношении индивидуальна для каждого из них Для того чтобы можно было установить для каж­дого объекта различия в количественном содержании свойства, отображаемого ФВ, в метрологии введены по­нятия ее размера и значения.

Размер физической величины — это ее количественная определенность, присущая конкретному материальному объекту, системе, явлению или процессу. Например, ка­ждое тело обладает определенной массой, вследствие че­го тела можно различать по их массе, т.е. по размеру ин­тересующей нас ФВ

Значение ФВ — это выражение ее размера в виде неко­торого числа принятых для нее единиц Оно находится пу­тем ее измерения или вычисления в соответствии с основ­ным уравнением измерения Q = q[Q], связывающим меж­ду собой значение ФВ Q, числовое значение q и выбранную для измерения единицу [Q1 данной величины В зависимости от размера выбранной единицы будет ме­няться числовое значение ФВ, тогда как размер этой вели­чины будет одним и тем же.

Единица ФВ — это ФВ фиксированного размера, ко­торой условно присвоено числовое значение, равное единице Она применяется для количественного выра­жения однородных ФВ Размер единиц ФВ устанавливается путем их законодательно закрепленного определе­ния метрологическими органами государства

Важнейшей характеристикой ФВ является ее размер­ность dimQ — выражение в форме степенного много­члена, составленного из произведений символов основ­ных ФВ в различных степенях и отражающего связь дан­ной ФВ с ФВ, принятыми в данной системе за основные с коэффициентом пропорциональности, равным 1:

dim Q = L^a M^b T^g I^h…, где L, М, Т, 1 — условные обозначе­ния основных величин, a, b, g, h— вещественные числа Показатель степени, в которую возведена размерность основной величины, называют показателем размерности. Если все показатели размерности равны нулю, то такую величину называют безразмерной.

Размерность ФВ является более общей характери­стикой, чем определяющее ФВ уравнение связи, по­скольку одна и та же размерность может быть присуща величинам, имеющим разную качественную природу и различающимся по форме определяющего уравнения.

Описание свойства, характеризуемого рассматривае­мой ФВ, осуществляется на языке других, ранее найден­ных величин.

Эта возможность обуславливается наличием объективно существующих взаимосвязей между свойства­ми объектов, которые, будучи переведенными на язык ве­личин, становятся моделями, образующими в своей сово­купности систему уравнений, описывающих данный раз­дел физики Различают два типа таких уравнений

1 Уравнения связи между величинами — это уравне­ния, отражающие связь между величинами, обусловлен­ную законами природы, в которых под буквенными сим­волами понимаются ФВ. Они могут быть записаны в ви­де, не зависящем от выбора единиц измерений входящих в них ФВ Q=KX^a Y^bZ ^g… Коэффициент К не зависит от выбора единиц измерений, он определяет связь между величинами/

2 Уравнения связи между числовыми значениями ФВ — это уравнения, в которых под буквенными символами понимают числовые значения величин, соответствующие выбранным единицам Вид этих уравнений зависит от выбранных единиц измерения. Они могут быть записаны в виде

Q = K_e KX^a Y^b Z^g…,

где К_e — числовой коэффициент пропорциональности, зависящий от выбранной системы единиц/

С помощью уравнений связи между числовыми значениями ФВ формулируются определении одних вели­чин на языке других и указываются способы их нахожде­ния Совокупность ФВ, образованная в соответствии с принятыми принципами, когда одни величины прини­маются за независимые, а другие являются функциями независимых величин, называется системой ФВ.

Обосновано, но в общем произвольным образом вы­бираются несколько ФВ, называемых основными Ос­тальные величины, называемые производными, выража­ются через них на основе известных уравнений связи между ними. Примерами производных величин могут служить плотность вещества, определяемого как масса вещества, заключенного в единице объема, ускорение -изменение скорости за единицу времени и др

В названии системы ФВ применяют символы вели­чин, принятых за основные Например, система величин механики, в которой в качестве основных используются длина (L), масса (М) и время (Т), называется системой LMT Действующая в настоящее время международная система единиц (СИ) должна обозначаться символами LMTIQNJ, обозначающими соответственно символы ос­новных величин, длины (L), массы (М) и времени (Т), си­лы электрического тока (I), температуры (Q), количества вещества (N) и силы света (J)

Совокупность основных и производных единиц ФВ, образованная в соответствии с принятыми принципами, называется системой единиц ФВ Единица основной ФВ в данной системе является основной единицей системы. В СНГ используется СИ, введенная ГОСТ 8.417-81 «ГСИ. Единицы физических величин». В качестве основных единиц приняты метр, килограмм, апмер, кельвин, моль и канделла (таб.3.1).

Производная единица системы единиц - это единица производной ФВ системы единиц, образованная в соот­ветствии с уравнением, связывающим ее с основными единицами или же с основными и уже определенными производными единицами. Производные единицы системы СИ, имеющие специальное название, приведены в табл. 3.2.

Для установления производной единицы следует:

• выбрать величины, единицы которых принимают­ся в качестве основных;

• установить размер этих единиц;

• выбрать определяющее уравнение, связывающее величины, измеряемые основными единицами, с вели­чиной, для которой устанавливается производная едини­ца. При этом символы всех величин, входящих в опреде­ляющее уравнение, должны рассматриваться не как сами величины, а как их именованные числовые значения;

• приравнять единице (или другому постоянному числу) коэффициент пропорциональности К_е, входящий в определяющее уравнение. Это уравнение следует запи­сывать в виде явной функциональной зависимости про­изводной величины от основных.

Установленные таким способом производные еди­ницы могут быть использованы для введения новых производных величин. Поэтому в определяющие урав­нения наряду с основными единицами могут входить и производные величины, единицы которых установлены ранее.

Таблица 3.1.