Свойства линейных кодов
1. Любые К линейно-независимых кодовых слов задают все множество 2кслов линейного кода и могут составить его образующую матрицу. Произвольная образующая матрица может быть приведена к каноническому виду суммированием строк по mod2.
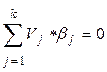 |
Кодовые слова Vj являются линейно-независимыми, если сумма по модулю 2 вида
только когда все коэффициенты bj равны 0.
2. Сумма по модулю 2 любого числа кодовых слов также является словом данного линейного кода.
3. Нулевая последовательность всегда является кодовым словом.
4. Кодовое расстояние dmin равно минимальному весу ненулевого кодового слова.
5.
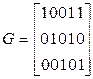 |
Из любого линейного (n,k) кода с кодовым расстоянием dmin можно получить код (n-i, k-i) с кодовым расстоянием не меньше dmin . Для этого из образующей матрицы G исходного кода вычеркивают любые i строк и i, ставших нулевыми столбцов. Например, задан код (5,3) с образующей матрицей G, кодовое расстояние которого равно dmin=2.
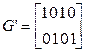 |
Получим укороченный код (4,2), вычеркнув первую строку и первый столбец, ставший нулевым, в матрице G. Образующая матрица укороченного кода G' имеет вид
Кодовое расстояние укороченного кода dmin=2.
Дата добавления: 2015-08-26; просмотров: 954;
