Сферический угол FCA между гринвичским меридианом и астрономическим меридианом точки А.

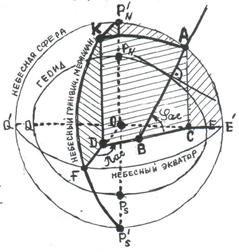
Для измерения астрономических координат точки А на небесной сфере производят следующие геометрические построения (рисунок 4.7):

Рисунок 4.7

1. Вокруг геоида производят построение небесной сферы, центр которой совпадает с центром геоида. В этом случае ось мира 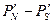совпадает с осью вращения Земли P_N-P_S, а плоскость небесного экватора совпадает с плоскостью земного экватора.

2. Из точки А небесной сферы проводят нормаль к поверхности геоида до пересечения с плоскостью небесного экватора и получают линию АВ, которая является вертикалью точки А.

3. Из точки А опускают перпендикуляр на плоскость небесного экватора и получают точку С, которая является проекцией точки А на плоскость небесного экватора, а линия ВС является проекцией вертикали точки А на плоскость небесного экватора.

4. Через треугольник АВС проводят плоскость ACDK, которая является плоскостью небесного астрономического меридиана точки А, а кривая АК – является небесным астрономическим меридианом точки А.

Таким образом, астрономическая широта ( 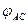) точки А небесной сферы – это плоский угол АВС между плоскостью небесного экватора и вертикалью данной точки.

Астрономическую долготу ( 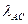) точки А небесной сферы определяют 3 угла:

1. Плоский угол FDC между плоскостью небесного гринвичского меридиана и проекцией вертикали точки А на плоскость небесного экватора.

2. Двугранный угол между плоскостью небесного гринвичского меридиана и плоскостью небесного астрономического меридиана точки А.

3. Сферический угол между небесным гринвичским меридианом и небесным астрономическим меридианом точки А.

Рисунок 4.8

Астрономические координаты точки определяют с помощью астрономических наблюдений на поверхности Земли.

Разница между астрономической широтой точки и географической широтой этой точки достигает : .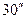

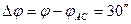Разница между астрономической долготой точки и географической долготой этой точки достигает : .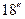

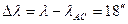Полярные координаты точки А (рисунок 4.8) – это угловая величина – полярный угол α и линейная величина – радиус-вектор ( 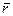), которые определяют положение точки на морской навигационной карте относительно полярной точки О и полярной оси ОР.

Полярная точка – это какая-либо фиксированная точка на морской навигационной карте, которой может быть, например, точка местоположения береговой радиолокационной станции (РЛС), которую на карте наносят с помощью условного знака РЛС (рисунок 4.9).

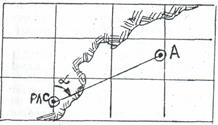
Рисунок 4.9

Радиолокационная станция (от лат. radio – испускаю лучи, т.е. радиоволны и locatio– расположение) или радар (от англ. RADAR – Radio Detection and Randing – радиообнаружение и измерение дальности) – это электронное устройство, которое предназначено для обнаружения различных объектов с помощью радиоволн и определения их местоположения путем измерения направления и расстояния до них.

Таким образом, если с помощью РЛС измерить полярный угол α и расстояние до судна, то проложив радиус-вектор 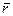из полярной точки (точки РЛС) под углом α к полярной оси (к линии истинного меридиана) – получают точку А – местоположение судна на карте.

ВЫВОДЫ

1. Географические координаты точки – это угловые величины – географическая широта и географическая долгота точки, которые определяют положение этой точки на поверхности земного сфероида относительно земного экватора и гринвичского меридиана.

2. Географическая широта точки – это плоский угол φ между плоскостью земного экватора и нормалью этой точки к поверхности земного сфероида.

Географическую широту точки можно измерить или вычислить с помощью дуги любого меридиана, которая заключена между земным экватором и параллелью этой точки.

3. Счет географической широты точки ведут от нуля градусов на земном экваторе до девяноста градусов в сторону северного истинного полюса и от нуля градусов на земном экваторе до девяноста градусов в сторону южного истинного полюса.

4. Географическая широта точки может иметь следующие наименования:

4.1 северная (С) широта точки или нордовая (N) широта точки – если эта точка находится в северном полушарии;

4.2 южная (Ю) широта точки или зюйдовая (S) широта точки – если эта точка находится в южном полушарии.

5. Географическая долгота точки – это двугранный угол λ между плоскостью гринвичского меридиана и плоскостью меридиана этой точки.

6. Плоскость гринвичского меридиана – это плоскость сечения земного сфероида, проходящая через гринвичский меридиан и ось вращения Земли.

7. Плоскость меридиана точки – это плоскость сечения земного сфероида, проходящая через меридиан этой точки и ось вращения Земли.

8. Географическую долготу точки можно измерить или вычислить двумя способами:

8.1 С помощью дуги земного экватора, которая заключена между гринвичским меридианом и меридианом этой точки.

8.2 С помощью сферического угла при северном истинном полюсе Земли между гринвичским меридианом и меридианом этой точки.

9. Счет географической долготы ведут от нуля градусов на гринвичском меридиане до ста восьмидесяти градусов в сторону востока и от нуля градусов на гринвичском меридиане до ста восьмидесяти градусов в сторону запада.

10. Географическая долгота точки может иметь следующие наименования:

10.1 Восточная (В) долгота точки или остовая (Е) долгота точки – если эта точка находится в восточном полушарии;

10.2 Западная (З) долгота точки или вестовая (W) долгота точки – если эта точка находится в западном полушарии.

11. Сферические координаты точки - – это угловые величины – сферическая широта и сферическая долгота точки, которые определяют положение данной точки на поверхности земного шара относительно земного экватора и гринвичского меридиана.

12. Сферическая широта точки– это плоский угол φ_сф между плоскостью земного экватора и радиусом земного шара в этой точке.

13.Сферическая долгота точки – это двугранный угол λ_сф между плоскостью гринвичского меридиана и плоскостью меридиана этой точки.

14. Геоцентрические координаты точки – это угловые величины – геоцентрическая широта и геоцентрическая долгота точки, которые определяют положение точки на земном сфероиде относительно центра этого эллипсоида.

15. Геоцентрическая широта точки – это плоский угол φ_гц между плоскостью земного экватора и радиусом-вектором земного эллипсоида в этой точке.

16. Радиус-вектор земного эллипсоида в какой-либо точке – это прямая, которая соединяет центр земного эллипсоида с данной точкой этого эллипсоида.

17. Разность между географической широтой какой-либо точки и геоцентрической широтой этой точки называется редукцией широты, величину которой вычисляют по формуле (4.1).

18. Редукция широты достигает наибольшей величины 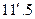на широте 45º.

19. Поскольку радиус-вектор земного эллипсоида в какой-либо точке находится в плоскости меридиана этой точки, то геоцентрическая долгота точки равна географической долготе этой точки.

20. Геодезические координаты точки – это угловые величины – геодезическая широта и геодезическая долгота точки, а также линейная величина – геодезическая высота, которые определяют положение точки Земной поверхности относительно поверхности земного эллипсоида.

21. Геодезическая широта точки Земной поверхности – это географическая широта проекции этой точки на поверхность земного сфероида.

22. Геодезическая долгота точки земной поверхности – это географическая долгота проекции этой точки на поверхность земного сфероида.

23. Проекция какой-либо точки земной поверхности на поверхность земного сфероида – это точка пересечения нормали этой точки к поверхности земного сфероида.

24. Геодезическая высота точки земной поверхности – это высота данной точки относительно поверхности земного сфероида, которую измеряют с помощью отрезка нормали этой точки к поверхности земного сфероида между земной поверхностью и поверхностью земного сфероида.

25. Астрономические координаты точки – это угловые величины – астрономическая широта точки и астрономическая долгота точки, которые определяют положение этой точки на поверхности геоида и на небесной сфере.

26. Астрономическая широта точки поверхности геоида – это плоский угол 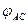между плоскостью земного экватора и вертикалью этой точки.

27. Астрономическая долгота точки поверхности геоида – это угол 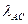, который имеет следующие определения:

27.1 Плоский угол между плоскостью гринвичского меридиана и проекцией вертикали этой точки на плоскость земного экватора.

27.2 Двугранный угол между плоскостью гринвичского меридиана и плоскостью астрономического меридиана этой точки.

27.3 Сферический угол между гринвичским меридианом и астрономическим меридианом этой точки. При этом:

27.3.1 Плоскость астрономического меридиана – это вертикальная плоскость, параллельная оси вращения Земли (перпендикулярная плоскости земного экватора).

27.3.2 Астрономический меридиан – это линия пересечения плоскости астрономического меридиана с поверхностью геоида.

28. Астрономическая широта точки небесной сферы – это плоский угол 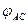между плоскостью небесного экватора и вертикалью этой точки.

29. Астрономическая долгота точки небесной сферы – это угол 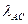, который имеет следующие определения:

29.1 Плоский угол между плоскостью небесного гринвичского меридиана и проекцией вертикали этой точки на плоскость небесного экватора.

29.2 Двугранный угол между плоскостью небесного гринвичского меридиана и плоскостью небесного астрономического меридиана этой точки.

29.3 Сферический угол между небесным гринвичским меридианом и небесным астрономическим меридианом этой точки. При этом:

29.3.1 Плоскость небесного астрономического меридиана – это вертикальная плоскость, параллельная оси мира (перпендикулярная плоскости небесного экватора).

29.3.2 Небесный астрономический меридиан – это линия пересечения плоскости небесного астрономического меридиана с небесной сферой.

30. Полярные координаты точки – это угловая величина – полярный угол α и линейная величина – радиус-вектор ( 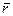), которые определяют положение этой точки на карте относительно фиксированной полярной точки и полярной оси.