Полигон распределения

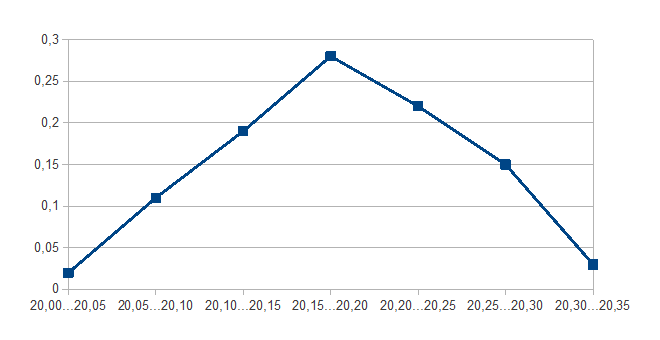
При большом числе измеряемых деталей и при большом числе интервалов размеров L ломаная эмпирическая кривая (полигон) приближается по форме к плавной кривой, называемой кривой распределения. На рисунке (см. выше) представлены гистограмма распределения и полигон распределения. Для построения гистограммы рекомендуется разбивать диапазон минимум на 6 интервалов (лучше 8...10) при общем числе измеряемых деталей не менее 50 штук.

При различных условиях обработки деталей рассеивание их действительных размеров подчиняется различным математическим законам. В технологии приборостроения большое практическое значение имеют: закон нормального распределения (закон Гаусса), закон равной вероятности, закон Максвелла, закон модуля разности и др.

Рассмотрим основные законы рассеивания:

1. Закон нормального распределения.Многочисленные исследования и практика показали, что распределение действительных размеров деталей, обрабатываемых на настроенных станках, подчиняется закону нормального распределения. Теоретическое обеспечение этому положению даёт центральная теорема теории вероятности, а именно — теорема Ляпунова, которая устанавливает общие условия, при которых суммы взаимонезависимых случайных слагаемых подчиняются закону нормального распределения.

Эти условия заключаются в следующем:

1) влияние каждого из слагаемых на сумму ничтожно мало и приблизительно одинаково по своей величине, т. е. среди слагаемых нет доминирующих.

2) в состав суммы входит большое число взаимонезависимых случайных величин.

При этом, в соответствии с законом нормального распределения, тем точнее, чем больше число слагаемых. При несоблюдении условий, выраженных в теореме Ляпунова, распределение действительных размеров деталей может подчиняться другим законам.

Так как результирующая погрешность обработки представляет собой сумму большого числа погрешностей, зависящих от станка, приспособления, инструмента и детали, которые, по существу, представляют собой взаимонезависимые случайные величины, и влияние каждой из них на результирующую погрешность имеет один порядок, то распределение результирующих погрешностей обработки детали подчиняется (на основе теоремы Ляпунова) закону нормального распределения.

Уравнение кривой нормального распределения имеет вид:

Y = 1 / (σ√2π) * e^{-(Li-Lср)² / 2σ²}

L_ср = Σ_iL_i * (m_i/n) = (1/n) * Σ_iL_im_i

σ = +√(Σ(L_i-L_ср)²*(m_i/n)) = +√((1/n)*Σ_i(L_i-L_ср)²*m_i)

где: L_ср — среднее арифметическое размеров деталей данной партии;

L_i — текущий действительный размер;

m_i — частота;

n — количество деталей в партии;

σ — среднее квадратичное отклонение;

e — основание натурального логарифма.

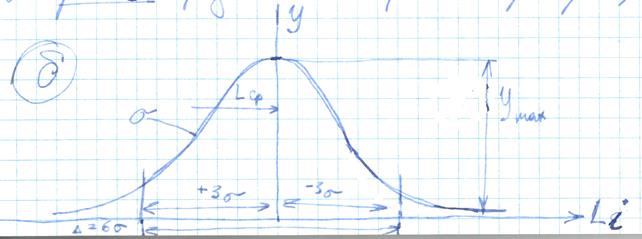
На рис. «б» представлена кривая нормального распределения:

[рисунок «б»]

Характеризуется:

1) среднекрадратическим, среднеарифметическим отклонением;

2) диапазоном рассеяния Δ.

Среднее арифметическое действительных размеров данной партии Lср характеризует положение центра группирования размеров. Кривая Гаусса асимптотически приближается к оси абсцисс. На расстоянии ±3σ от вершины кривой её ветви так близко подходят к оси абсцисс, что вся площадь под кривой в пределах ±3σ даёт 99,73% всей возможной площади под кривой.

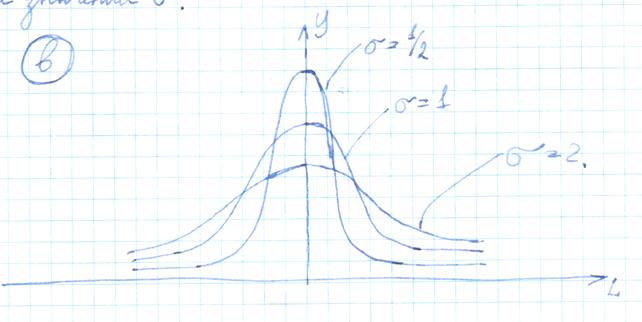
На рис. «в» представлены кривые нормального распределения, имеющие различные значения σ.

[рисунок «в»]

С изменением величины σ меняется размах кривой. При действии закона нормального распределения:

Δ = 6σ