Глава 1. Матрицы

Раздел 1. Линейная и векторная алгебры

МатрицейА называется таблица чисел. Если матрица состоит из m строк и n столбцов, то говорят, что размерность матрицы есть m на n. Количество элементов в такой матрице равно произведению mn. Обозначение матрицы

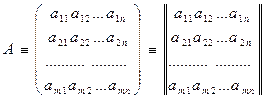(1.1)

или сокращенно A=(a_ij)_{m n}. Числа a_ij, составляющие матрицу, называются ее элементами. Первый индекс указывает номер строки, второй - номер столбца.

Матрица называется прямоугольной,если mn, Если m=n, то матрица называется квадратной и число n - порядком матрицы. Матрица, содержащая один столбец, называется матрица-столбец. Матрица, состоящая из одной строки - матрица-строка. У таких матриц элементы могут иметь только один номер.

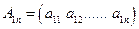; (1.2)

Матрица, все элементы которой равны нулю, называется нулевой матрицей.

Для квадратной матрицы порядка n (число строк равно числу столбцов и равно n) A=(а_ij)_n,n, элементы a₁₁, a₂₂, ..., a_nn с одинаковыми индексами образуют главную диагональ. Элементы a_{1 n}, a_{2 n-1}, ..., a_{n 1} образуют побочную диагональ. Квадратная матрица называется диагональной, если все элементы, стоящие вне главной диагонали, равны нулю: a_ij=0 при ij. Диагональная матрица обозначается так

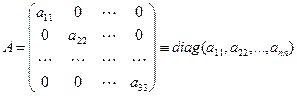. (1.3)

Диагональная матрица, у которой все диагональные элементы равны, единице называется единичнойи обозначается

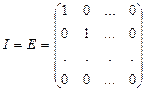(1.4)

Квадратная матрица называется треугольной, если все элементы, стоящие ниже (или выше) главной диагонали, равны нулю:

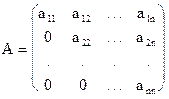, . (1.5)

Каждой квадратной матрице ставится в соответствие число, называемое детерминантомили определителем,которыйобозначается символами detA или D(A) или |a_ij|.

Для матрицы 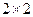определитель находится по формуле: произведение элементов главной диагонали минус произведение элементов побочной диагонали

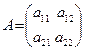det(A) = 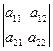= a₁₁ a₂₂ – a₁₂ a_21. (1.6)

Для матрицы 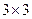определитель находится по формуле

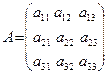det(A) = = a₁₁ a₂₂ a₃₃ + a₁₂ a₂₃ a₃₁ + a₁₃ a₂₁a₃₂ - a₁₃a₂₂ a₃₁ –

- a₁₂ a₂₁ a₃₃ - a₁₁a₂₃ a_32. (1.7)

Пример. Вычислить определитель матрицы .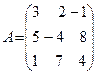

Решение:

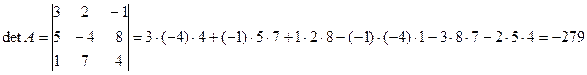
Определитель единичной матрицы равен единице det I = 1.

Минором M_ik называется определитель меньшего порядка (размера), полученный при вычеркивании i-той строки и k-того столбца.

Алгебраическим дополнением A_ik называется минор, знак которого определяется по правилу A_ik = (-1)^i+k M_ik.

Определитель можно представить в виде суммы произведений элементов любой строки или столбца на их алгебраические дополнения, например

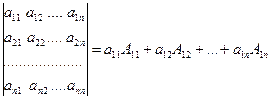, (1.8)

где

, ,……. .

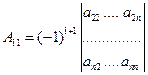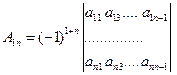Квадратная матрица называется невырожденной (неособенной), если det A¹0, и вырожденной(особенной), если det A=0. Определитель треугольной матрицы равен произведению диагональных элементов:

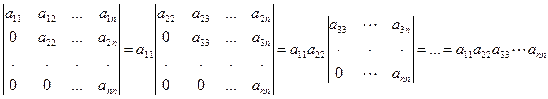. (1.9)