Краткие сведения из теории фильтров

Фильтры — неотъемлемая часть многих СВЧ устройств. Они используются для целей разделения и суммирования сигналов с различными частотами в многоканальных устройствах, в преобразователях и умножителях частоты, для повышения избирательности приемных устройств, для ограничения спектра передатчика и т. д.

Столь широкое применение фильтров в технике СВЧ привело к большому многообразию их схем и конструкций. Наибольшее распространение нашли фильтры СВЧ, полученные из низкочастотных фильтров путем замены элементов с сосредоточенными параметрами элементами СВЧ устройств, обладающих теми же характеристиками в определенной области частот.

Фильтры СВЧ, как и фильтры с сосредоточенными параметрами, представляют собой один или N последовательно соединенных четырехполюсников, избирательно пропускающих определенную полосу частот. В зависимости от полосы пропускания фильтры разделяются на следующие типы:

фильтры нижних частот (ФНЧ), пропускающие частоты от нуля до частоты среза - f₁ (рис 4.1, а);

фильтры верхних частот (ФВЧ), пропускающие частоты от f₁ до 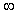(рис.4.1, б);

полосовые фильтры (ПФ), пропускающие определенную полосу частот от f_-nдо f_n(рис. 4.1, в);

заграждающие (режекторные) фильтры (ЗФ), не пропускающие полосу частот от f_-з до f_з (рис. 4.1, г).

Практически такие идеальные частотные характеристики неосуществимы, поэтому при проектировании фильтров задаются отклонения от этих идеальных характеристик.

Каждый фильтр характеризуется следующими параметрами:

граничные частоты полосы пропускания f_-n, f_n (для ФНЧ и ФВЧ —

частоты среза f₁);

граничные частоты полосы загражденияf_-з, f_з;

максимально допустимое затухание в полосе пропускания - b_n, дб;

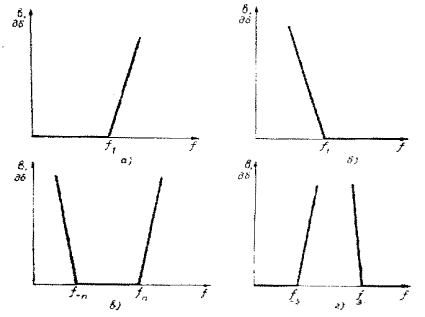
Рис. 4.1.Идеальные частотные характеристики фильтров:

а - ФНЧ; б - ФВЧ; в - ПФ; г - ЗФ.

минимальное затухание на границах полосы заграждения - b_n, дб;

номинальное характеристическое сопротивление, выбираемое из конструктивных соображений.

В зависимости от предъявляемых требований к фильтру применяются различные схемы фильтров и разнообразное их конструктивное выполнение. У полосовых фильтров наибольшее распространение получили следующие схемы звеньев:

трехэлементная схема (рис. 4.2, а, Т-образная схема);

четырехэлементная схема (рис. 4.2, б, П-образная схема}.

Каскадное соединение этих звеньев образует общую лестничную структуру фильтра (рис. 4.2, в, г).

Задачей проектирования является обеспечение требуемой полосы пропускания, допустимых уровней затухания в полосе пропускания, обеспечение требуемого динамического диапазона, минимального веса и габаритов, сохранение работоспособности в ухудшенных климатических условиях, простоты настройки и изготовления и максимальной надежности.

Существуют два метода расчета фильтров:

по характеристическим параметрам;

по рабочим параметрам.

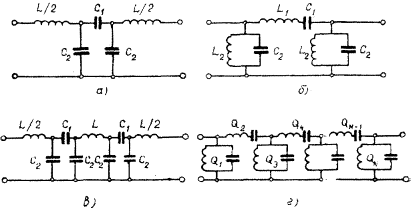
Рис. 4.2.Схемы фильтров: а —трехэлементная схема звена;

б — четырехэлементная схема звена;в, г —- лестничные схемы фильтров трех- и четырехэлементные соответственно.

Все расчеты по характеристическим параметрам являются частными случаями расчетов по рабочим параметрам, а следовательно, более просты. Метод расчета по характеристическим параметрам применяется в том случае, если допускается значительная неравномерность характеристики частотного затухания фильтра в полосе прозрачности. В этом случае фильтр состоит из N одинаковых звеньев. Параметром является характеристическое сопротивление фильтра, выбираемое из конструктивных соображений и используемое для определения элементов схемы фильтра. По методу характеристических параметров рассчитываетсятрехэлементная схема (рис. 4.2, а, в), выполненная на коаксиальных линиях и получившая наибольшее практическое распространение.

Метод расчета по рабочим параметрам позволяет получить заданную частотную характеристику фильтра при минимальном числе элементов, исходя из условий физической реализуемости. В качестве рабочих параметров используются следующие: требуемая полоса пропускания — f_-n>f_n; максимально допустимое затухание в полосе пропускания — b_n; минимально допустимое затухание в полосе заграждения — b_з. Требуемая частотная характеристика затухания аппроксимируется физически реализуемой функцией, через параметры которой определяются элементы схемы фильтра.

Существует несколько способов аппроксимации:

аппроксимация с помощью максимально гладкой кривой, описываемойполиномом Баттерворса,

аппроксимация с помощью полиномов Чебышева,

аппроксимация с помощью эллиптической функции Якоби.

Наибольшее распространение получили первые два способа аппроксимации.

При аппроксимации с помощью максимально гладкой (плоской) кривой частотная характеристика полосового фильтра имеет вид, показанный на рис.4.3, а (парабола 2 N-го порядка). В этом случае частотная характеристика описывается формулой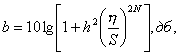

где

(4.2)

S - масштабный множитель,

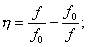(4.3)

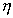- частотная переменная;

f₀ - средняя частота диапазона;

N - число звеньев фильтра;

h - амплитудный множитель;

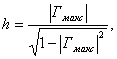(4.4)

Г_макс - максимально допустимый коэффициент отражения в полосе f_-n>f_n, связанный с максимально допустимыми потерями в полосе пропускания формулой

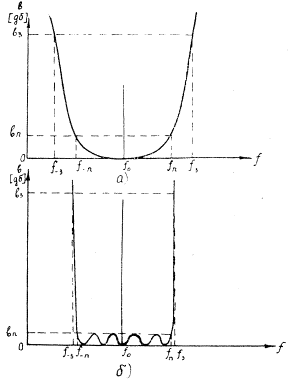
Рис. 4.3. Частотные характеристики полиномиальных полосовыхфильтров: а - максимально гладкая; б - чебышевская.

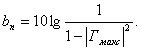(4.5)

При аппроксимации с помощью полиномов Чебышева частотная характеристика имеет вид, показанный на рис.4.3, б. В этом случае частотная характеристика описывается формулой

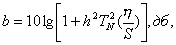(4.6)

где 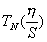-полином Чебышева 1-го рода, N-го порядка, (2.9) - (2.12);

N — число звеньев фильтра.

Чебышевские фильтры имеют более крутые склоны частотной характеристики, чем фильтры с максимально гладкой характеристикой. Выбор того или иного типа частотной характеристики определяется заданными требованиями к фильтру. По выбранному типу частотной характеристики и заданным f_-n, f_n,f_-з, f_з, b_n, b_з определяется число звеньев фильтра N.

Для полосового фильтра число звеньев определяется по формулам:

для максимально гладкого фильтра

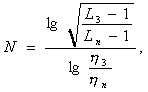(4.7)

где L_з, L_п - коэффициенты передач, определяемые из формул

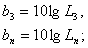
для чебышевского фильтра 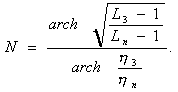(4.8)

Следующим этапом синтеза является определение численных значений элементов схемы фильтра. Для упрощения методики расчета по рабочим параметрам используется нормализованный расчет, то есть для «прототипа» — фильтра нижних частот (рис. 4.4), из которого можно получить элементы схемы проектируемого фильтра.

Элементы «прототипного» ФНЧ для фильтров с максимально гладкой характеристикой определяются по формуле

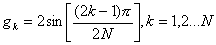(4.9)

Для фильтра с чебышевской формой характеристики элементы прототипа определяются из следующих выражений:

1) для нечетных ,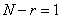

для четных ,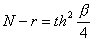

2)

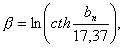
где b_n — максимально допустимая пульсация в полосе пропускания фильтра, дб (рис. 4.3);

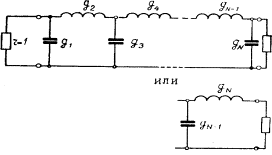
Рис. 4.4. Схема прототипа фильтра нижних частот для четных и нечетных N.

3)

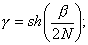
4)

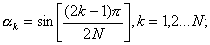
5) 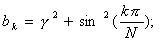(4.10)

6)

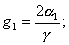
7)

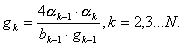
Приведенные формулы выведены при следующих предположениях:

1. Сопротивление нагрузки в левой части схемы равно 1 Ому.

2. Первый элемент g₁ — шунтирующая емкость в фарадах, последовательные элементы — индуктивности в генри.

3. Сопротивление r в правой части схемы равно 1 Ому для всех рассматриваемых случаев. Исключение представляют чебышевские фильтры с четным N.

Элементы схем других фильтров определяются через известные элементы прототипа путем соответствующих преобразований. Формулы для этих преобразовании разработаны для конкретныхсхем.

После расчета элементов фильтра остается задача его реализации с помощью элементов СВЧ. Методы реализации фильтров с помощью элементов СВЧ будут освещены в следующих разделах при рассмотрении типичных схем фильтров.