ПЕРЕДМОВА
Макросвіт і мікросвіт, їх взаємозв'язок. Сучасна картина світу
Фізика - це наука про природу. Вона виникла, як результат споконвіч-ного прагнення людей зрозуміти й описати світ, що її оточує. Світ надзви-чайно складний і цікавий. Людина, як частина цього світу завжди намага-лася зрозуміти його будову. Чи можливо його пізнати? Сьогодні ми зна-ємо, що світ пізнаваний і що багато чого вже відомо.
Найважливішим є те, що всі навколишні тіла складаються з атомів . Атоми є цеглинками світобудови, вони знаходяться у безперервному русі, притягаються на великих відстанях, але відштовхуються, коли їх нама-гатися наблизити один до одного. Розміри атомів приблизно 10–10 м.
Чи можна побачити атом? Можна – у тунельний мікроскоп (1981 р.) . Дивлячись у такий мікроскоп, можна перерахувати атоми поштучно (рис.1).
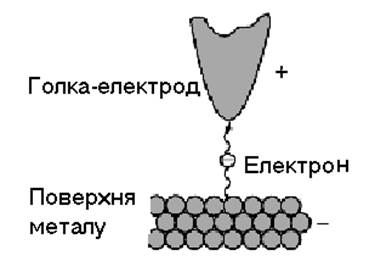
Рис. 1. Тунельний мікроскоп. Тунельний струм залежить від відстані між голкою й поверхнею
Чи є користь від того, що світ складається з атомів? Користь дуже велика. Лише в цьому випадку можна зрозуміти чому існують тверді, рідкі й газоподібні тіла; з якою швидкістю поширюється звук; чому летить літак; що таке температура і багато іншого.
А з чого складаються атоми? Атоми складаються з позитивно зарядженого ядра й негативно заряджених електронів, які рухаються навколо нього.
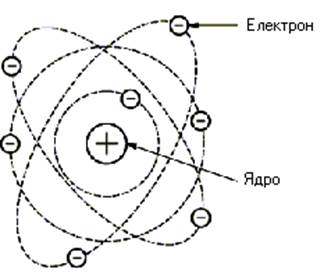
Рис. 2.Структура атома
Розміри електронів до цьго часу не піддаються вимірюванню. Відомо лише, що радіус електрона менший 10–18 м. Розмір ядра набагато більший, і має порядок 10–4÷ 10–5 Å або 10–14÷ 10–15 м. У свою чергу, ядра складаються із протонів і нейтронів.
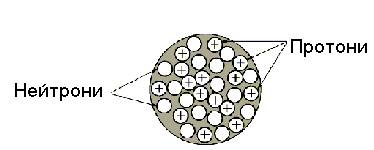
Рис. 3. Структура ядра
Уся маса атома зосереджена в ядрі. Електрон майже в 2000 разів легший від протона й нейтрона:
mp ≈ mn ≈ 1,67· 10–27 кг. (1)
Можна поставити ще й таке запитання “А з чого складаються протони й нейтрони?” Відповідь відома. Вони складаються з кварків. А електрон? Сам по собі він ні з чого не складається. Однак зупинимося поки що на цьому, інакше можна досить швидко підійти до межі незвіданого.
Атом порожній. Якщо ядро атома збільшити до розмірів яблука, то відстань від ядра до електронів буде порядку 1 км. Якби електрони і ядра не мали заряду, атоми спокійно проходили б один крізь інший, зовсім не заважаючи один одному.
Де все це знаходиться? Де розігруються всі явища природи? Весь цей простір називається Всесвітом. Розміри Всесвіту мають порядок 1030 м або приблизно 1010 світлових років . Для порівняння, відстань від Землі до Сонця дорівнює 1,5· 1015 м (150 млн. км.), а радіус Землі дорівнює 6,4· 106 м (6400 км). Загальне число протонів і нейтронів у Всесвіті дорівнює 1080 (1078÷ 1082). До складу Сонця входять близько 1057 протонів і нейтронів, у складі Землі їх - 4· 1051. Число зірок із масою порядку маси Сонця приблизно дорівнює 1023 . Зірка має масу від 0,01 до 100 мас Сонця.
Усе в природі складається з атомів, у тому числі і люди. Життя - це найбільш складне явище у Всесвіті. Людина, як одна з найбільш складних живих істот, складається з ≈ 1016 клітин. Клітина є елементарним фізіологічним осередком, який містить 1012 ÷ 1014 атомів. У будь-яку клітину будь-якого живого організму входить хоча б одна довга молекулярна нитка ДНК (дезоксирибонуклеїнової кислоти). У молекулі ДНК 108÷ 1010 атомів, точне розташування яких може змінюватися від індивідууму до індивідууму. Можна сказати, що молекула ДНК є носієм генетичної інформації.
Невіддільним від атомів є поняття взаємодії. Як атоми скріплюються між собою у твердому тілі? Чому Земля рухається навколо Сонця по коловій орбіті, а не летить від нього? Нарешті, чому протони в ядрі, маючи позитивний заряд, не відштовхуються один від одного і не розлітаються? Що тримає їх разом?
У даний час у природі виявлено чотири основних види взаємодії: електромагнітна, гравітаційна, сильна й слабка.
Перший вид взаємодії відбувається між зарядженими частинками. Коли пальцем намагатися натиснути на стіл, то будемо мати справу з взаємодією електромагнітної природи. Є притягання і є відштовхування.
Гравітаційна взаємодія, основним проявом якої є закон всесвітнього тяжіння, проявляється завжди у вигляді притягання (гравітаційне відштовхування поки що не виявлене). Свідченням цього є ті ж яблука, які завжди падають на Землю. Притягання між Землею й Сонцем змушує Землю рухатися по коловій орбіті навколо Сонця. Сила тяжіння - це та сила, яка змушує світитись зірки. Вона надає ядрам атомів необхідну для зближення кінетичну енергію (для подолання сили електpичного відштовхування), щоб змогла розпочатися реакція термоядерного синтезу - основного джерела енергії більшості зірок у Всесвіті.
Сильна взаємодія, на відміну від перших двох, є дуже короткодію-чою. Радіус дії сильної взаємодії не перевищує радіуса ядра і має порядок 10–14÷ 10–15 м. Ця взаємодія проявляється між нуклонами, тобто протонами й нейтронами, і завжди має характер притягання.
Нарешті, остання взаємодія - це слабка взаємодія. За допомогою слабкої взаємодії поглинається речовиною така невловима частинка як нейтрино. Прикладом процесу, у якому відбувається слабка взаємодія, є так званий β-розпад нейтрона. З урахуванням слабкої взаємодії вільний нейтрон нестабільний і розпадається на протон, електрон і антинейтрино приблизно через 15 хвилин:
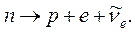 (2)
(2)
Останнім часом завдяки зусиллям теоретиків вдалося об'єднати електромагнітну й слабку взаємодії в одну, що зменшує число основних взаємодій до трьох. Порівняльна сила цих взаємодій така: якщо вважати, що відносна величина взаємодії нуклонів (протонів і нейтронів) у ядрі дорівнює одиниці, то наступною за величиною буде електромагнітна взаємодія - 10–2, потім слабка - 10–5. Найслабшою в цьому випадку є гравітаційна взаємодія ~ 10–40.
Природа сильної взаємодії усе ще залишається не повністю зрозумілою. Точніше, її теорія усе ще недобудована. Проте, людство вже навчилося використовувати ядерні сили, створивши атомну бомбу. Природа давно навчилася використовувати ці сили. Термоядерна реакція на Сонці - джерело тепла на Землі, причина свічення зірок у нічному небі, завдяки чому ми бачимо зірки, що знаходяться від нас на відстані в тисячі й мільйони світлових років.
Одним із найважливіших понять, введених у сучасну фізику, є поняття поля. Простір, у якому немає частинок і тому його можна назвати «порожнім», насправді не є таким. У «порожньому» (від частинок) просторі можуть існувати різні поля, прикладом яких є електромагнітне поле. Ці поля можуть існувати цілком самостійно, незалежно від частинок, які їх породжують. Ця форма існування - тепер добре відомі електромагнітні хвилі. Електромагнітні хвилі ввійшли в наше повсякденне життя. Радіо й телебачення здаються нам настільки ж природними як і автомобіль.
Гравітаційні хвилі поки що не виявлені експериментально, але їх існування впевнено пророкує загальна теорія відносності Ейнштейна. І, очевидно, їх виявлення не за горами. Уже тепер є реальним створення надчутливих детекторів гравітаційних хвиль, які здатні зареєструвати вибух наднових зірок у Галактиці, віддаленої від нас на відстань у мільйони світлових років. І тоді одночасно зі спалахом світла до нас дійде гравітаційна хвиля, яка теж поширюється зі швидкістю світла. Збіг у часі цих подій буде переконливим доказом існування гравітаційних хвиль.
Основною рушійною силою майже всіх процесів, які відбуваються на Землі, є електромагнітні сили і явища, що ними породжені. Знання цих сил є основою для розуміння хімічних реакцій, біологічних процесів, а значить і життя, руху повітря, води і навіть землетрусів. І все це ховається в такій малесенькій часточці, як атом, що складається з позитивно зарядженого ядра і негативно заряджених електронів, які рухаються навколо нього.
Але чому електрони не падають на ядро, адже вони до нього майже доторкаються? Можна було б думати, що причина та ж, що і при обертанні Землі навколо Сонця. Земля обертається і не падає. Але тут є одна проблема. Річ у тому, що електрично заряджена частинка, рухаючись із прискоренням, випромінює електромагнітні хвилі. Ці хвилі несуть із собою енергію. У результаті електрон повинен, зрештою, впасти на ядро, а цього не відбувається - атом відносно стійкий (наше з вами існування - тому доказ). У чому ж причина стабільності атома? Справа в тім, що закони, які керують рухом електрона навколо ядра атома, - це не ті закони класичної механіки, завдяки яким Земля рухається навколо Сонця. В атомі діють закони квантової механіки.
Квантова механіка, або квантова фізика - одне з найбільших наукових досягнень двадцятого століття. Вона описує закони руху частинок у мікросвіті, тобто рух частинок малої маси ( або електронів атома) у малих ділянках простору. Квантова механіка - це більш загальна наука, яка включає в себе класичну механіку як окремий випадок. До чого ж зводиться основне твердження квантової механіки? Воно зводиться до того, що частинки не можуть мати одночасно визначені значення координат й імпульсу, тобто у квантовій механіці не існує поняття траєкторії частинки. Якщо Δ x - це невизначеність координати частинки, а Δ p - невизначеність її імпульсу, то ці величини в квантовій механіці обмежені нерівністю
Δ x Δ p ≥ ħ. (3)
де ħ - постійна Планка (ħ = 1,054· 10–34 Дж·с).
Це співвідношення, називається співвідношенням невизначеності Гейзенберга. Суть цього співвідношення полягає в тому, що якби електрон упав на ядро (а воно дуже маленьке), то його координата визначалася б із точністю Δ x = 0. Але в цьому випадку невизначеність імпульсу Δ p буде дорівнювати безмежності і електрон з такою енергією вилетів би з ядра знову, переборовши сили притягання. Неможливість локалізації електрона на ядрі є в остаточному підсумку наслідком того, що насправді електрон - не частинка, а хвиля, довжина якої
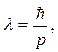 (4)
(4)
де p — імпульс електрона.
А, як відомо, хвилю не можна локалізувати в просторі з розмірами, меншими за довжину хвилі. З цих міркувань можна оцінити розмір атома.
Скористаємося співвідношенням невизначеності Δ r Δ p ≈ ħ, де Δ r — невизначеність координати електрона, а Δ p — невизначеність його імпульсу. Будемо вважати, що величини Δ r ≈ r і Δ p ≈ p, де r - характерна відстань електрона від ядра (тобто розмір атома), а p - значення імпульсу електрона на цій відстані. При русі електрона в кулонівському полі ядра, потенціальна енергія буде такого ж порядку, що й кінетична енергія. Тому маємо два співвідношення для визначення p і r:
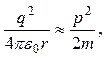 (6)
(6)
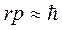 .
.
З першої умови одержуємо, що 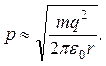 Підставивши цей вираз у друге рівняння, знайдемо радіус атома
Підставивши цей вираз у друге рівняння, знайдемо радіус атома
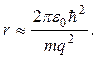 (7)
(7)
Приблизно ħ ≈ 10–34 Дж·с, m ≈ 10–31 кг і q ≈ 1,6· 10–19 Кл. Підставля-ючи ці величини у формулу (7), одержуємо 0,4 Å.
Таким чином, атом є досить стійким завдяки існуванню принципу невизначеності. Квантова механіка необхідна для розуміння хімічних і біологічних процесів, а значить для розуміння того, як ми улаштовані. Однак, унаслідок її відносної складності, починають вивчати фізику з більш простих речей - із класичної механіки.
ЛЕКЦІЯ 1
КІНЕМАТИКА
1.1.Кінематика руху матеріальної точки. Системи координат. Переміщення і швидкість руху. Пройдений шлях. Середні значення кінематичних величин.
1.2. Рух точки по колу. Кутова швидкість і кутове прискорення.
1.3. Тангенціальне і нормальне прискорення. Зв’язок між кінематичними величинами криволінійного руху.
1.1. Кінематика руху матеріальної точки. Системи координат.
Переміщення і швидкість руху. Пройдений шлях. Середні значення кінематичних величин
Кінематикою називають розділ механіки, в якому вивчається рух тіл без вияснення причин цього руху.
Механічним рухом тіла називають зміну його положення в просторі по відношенню до інших тіл протягом певного часу.
Механічний рух є відносним. Рух одного і того ж тіла відносно різних тіл може бути різним. Тому для пояснення руху тіла слід вказувати тіло відліку, тобто тіло, відносно якого розглядається рух в просторі й часі. З тілом відліку зв’язують систему координат.
Системою координат називають три взаємно перпендикулярні осі, початок яких суміщається з тілом відліку. Таку систему координат називають декартовою.
Положення довільної точки М в просторі характеризується радіусом-вектором 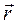 , який з’єднує початок координат з точкою М в просторі (рис.1.1).
, який з’єднує початок координат з точкою М в просторі (рис.1.1).
З рисунку видно, що
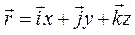 , (1.1.1)
, (1.1.1)
де 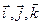 - одиничні вектори, напрямки яких збігаються з напрямками відповідних осей координат x, y, z. Модуль радіуса-вектора дорівнює
- одиничні вектори, напрямки яких збігаються з напрямками відповідних осей координат x, y, z. Модуль радіуса-вектора дорівнює
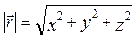 . (1.1.2)
. (1.1.2)
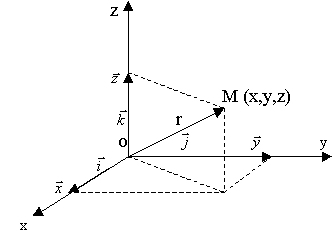
Рис.1.1
Рух матеріальної точки М(x,y,z) повністю буде визначено, якщо декартові координати матеріальної точки будуть задані в залежності від часу:
x = x(t); y=y(t); z=z(t) . (1.1.3)
Ці рівняння називаються кінематичними рівняннями руху точки, вони еквівалентні одному векторному рівнянню руху
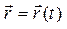 . (1.1.4)
. (1.1.4)
Будь-яке тіло має відповідні розміри. Тому різні частини тіла можуть перебувати в різних точках простору. Якщо розміри тіла малі в порівнянні з відстанями до інших тіл, то дане тіло можна вважати матеріальною точкою. Якщо всі частини тіла рухаються однаково, то такий рух називається поступальним. Прикладом поступального руху може бути рух автомобіля на горизонтальній ділянці шляху. При поступальному русі тіла його можна розглядати як матеріальну точку.
Поняття матеріальної точки відіграє дуже важливу роль, значно спрощуючи розуміння кінематику руху матеріальної точки. Переміщуючись у просторі з однієї точки в іншу, тіло описує деяку лінію, яку називають траєкторією руху тіла. Рівняння траєкторії руху можна одержати, якщо з кінематичних рівнянь (1.1.3) виключити час t.
У залежності від форми траєкторії, рух матеріальної точки, або твердого тіла, може бути прямолінійним і криволінійним. При прямолінійному русі вектор переміщення збігається з напрямком руху, а при криволінійному русі напрям вектора переміщення може бути під довільним кутом до напрямку руху.
Довжина шляху точки визначається сумою довжин всіх ділянок траєкторії, пройденої точкою за відповідний проміжок часу t.
DS=DS(t). (1.1.5)
Довжина шляху – скалярна функція часу.
Переміщенням точки 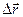 називають спрямований відрізок прямої, який з’єднує початкове положення точки з його наступним положенням. Переміщення точки є векторною величиною (рис.1.2).
називають спрямований відрізок прямої, який з’єднує початкове положення точки з його наступним положенням. Переміщення точки є векторною величиною (рис.1.2).
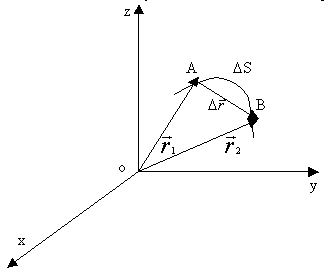
Рис.1.2
З рис. 1.2 видно, що
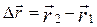 , (1.1.6)
, (1.1.6)
де 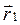 - радіус-вектор точки А,
- радіус-вектор точки А, 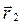 -радіус-вектор точки В.
-радіус-вектор точки В.
Якщо час Dt руху точки від А до В прямує до нуля, то довжина шляху DS буде наближатися до довжини вектора переміщення.
Для характеристики руху матеріальної точки вводиться поняття середньої швидкості
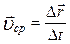 . (1.1.7)
. (1.1.7)
Вектором середньої швидкості за час Dt називається відносне переміщення 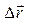 радіуса-вектора точки до проміжку часу Dt. Одиницею вимірювання швидкості є м/с.
радіуса-вектора точки до проміжку часу Dt. Одиницею вимірювання швидкості є м/с.
У кінематиці руху більше уваги приділяється не середній швидкості, а миттєвій.
Миттєва швидкість визначається границею, до якої наближається відношення (1.1.7) за безмежно малий проміжок часу, тобто
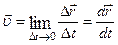 . (1.1.8)
. (1.1.8)
Вектор миттєвої швидкості збігається з дотичною до траєкторії руху і направлений в сторону руху.
Модуль миттєвої швидкості є скалярною величиною і дорівнює першій похідній шляху за часом
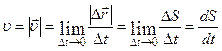 , (1.1.9)
, (1.1.9)
звідки
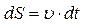 .
.
Якщо рух нерівномірний, то вводять поняття модуля миттєвоїшвидкості, величина якої змінюється з часом. В цьому випадку середню швидкість нерівномірного руху визначають за формулою:
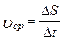 . (1.1.10)
. (1.1.10)
Довжина шляху S, пройденого точкою за проміжок часу від t1 до t2, визначається інтегралом
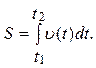 (1.1.11)
(1.1.11)
При прямолінійному русі точки напрям вектора швидкості залишається незмінним. Рух точки називається рівномірним, якщо модуль її швидкості не змінюється з часом. Для такого руху 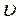 =const, a
=const, a
S=uDt. (1.1.12)
Якщо модуль швидкості збільшується з часом, то такий рух називається прискореним, якщо ж він зменшується, то він називається сповільненим.
Прискорення- це векторна величина, яка характеризує швидкість зміни швидкості по модулю і за напрямком.
Середнє прискорення матеріальної точки в інтервалі часу Dt є векторною величиною, рівною відношенню зміни швидкості 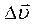 за час Dt:
за час Dt:
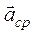 =
= 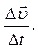 (1.1.13)
(1.1.13)
Миттєве прискорення матеріальної точки в інтервалі часу 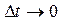 визначається похідною вектора швидкості за часом:
визначається похідною вектора швидкості за часом:
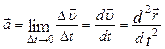 . (1.1.14)
. (1.1.14)
1.2. Рух точки по колу. Кутова швидкість і кутове прискорення
Довільний криволінійний рух можна подати як рух по дугах кіл. Тому зупинимося на кінематиці обертального руху, або руху точки вздовж колової траєкторії. У даному випадку зручно користуватись полярною системою координат, координатами якої є радіус кола R і кут повороту радіуса відносно вибраного напрямку j . В цьому випадку R – відстань від центра кола до точки на коловій траєкторії, а j - полярний кут (кут обертання)
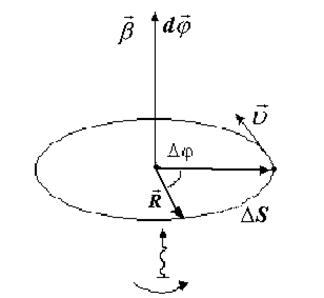
Рис.1.3
З рис. 1.3 видно , що 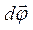 - кутове переміщення – векторна величина, модуль якої дорівнює куту повороту радіуса вектора
- кутове переміщення – векторна величина, модуль якої дорівнює куту повороту радіуса вектора 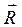 за час dt. Напрям цього вектора збігається з напрямком поступального руху правого гвинта.
за час dt. Напрям цього вектора збігається з напрямком поступального руху правого гвинта.
Кутова швидкість – векторна величина, яка дорівнює зміні кута повороту радіуса - вектора 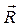 з часом, тобто
з часом, тобто
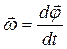 . (1.2.1)
. (1.2.1)
Напрям вектора 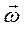 збігається з напрямком
збігається з напрямком 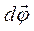 . Одиницею вимірювання кутової швидкості є рад/с.
. Одиницею вимірювання кутової швидкості є рад/с.
Кутове прискорення – векторна величина, яка дорівнює зміні кутової швидкості з часом, тобто
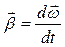 . (1.2.2)
. (1.2.2)
Напрям вектора кутового прискорення направлений по осі обертання (рис. 1.3). Вектор кутового прискорення руху точки по колу 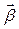 збігається з напрямком
збігається з напрямком 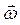 . Для сповільненого обертання вектор
. Для сповільненого обертання вектор 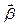 має протилежний напрям до вектора
має протилежний напрям до вектора 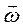 . Вимірюється кутове прискорення у рад/с2.
. Вимірюється кутове прискорення у рад/с2.
Модуль вектора лінійної швидкості точки 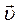 , напрям якої збігається з дотичною до кола, зв’язаний з модулем вектора кутової швидкості
, напрям якої збігається з дотичною до кола, зв’язаний з модулем вектора кутової швидкості 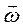 співвідношенням:
співвідношенням:
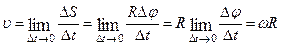 . (1.2.3)
. (1.2.3)
У векторній формі вектор швидкості 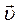 дорівнює векторному добутку векторів
дорівнює векторному добутку векторів 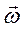 і
і 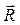
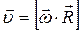 . (1.2.4)
. (1.2.4)
З визначення векторного добутку модуль вектора швидкості 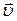 визначається співвідношенням
визначається співвідношенням
ê 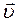 ê =wR sina , (1.2.5)
ê =wR sina , (1.2.5)
де a - кут між векторами 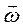 і
і 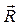 , як це показано на рис. 1.4.
, як це показано на рис. 1.4.
Для рівномірного обертання матеріальної точки по коловій траєкторії модуль кутової швидкості дорівнює
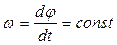 . (1.2.6)
. (1.2.6)
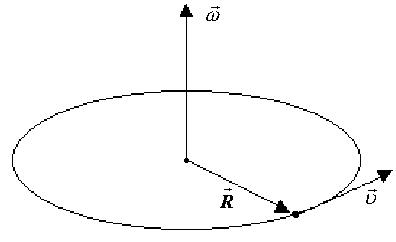
Рис.1.4
Рівномірний рух по колу можна характеризувати також періодом обертання Т, тобто часом, за який точка здійснює один повний оберт, 2p = wТ. Звідки
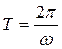 . (1.2.7)
. (1.2.7)
Частота обертання визначається числом повних обертів, які здійснює точка при русі по колу, за одиницю часу:
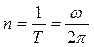 . (1.2.8)
. (1.2.8)
При рівноприскореному обертальному русі b = const. Тому формули кінематики обертального руху точки матимуть вигляд:
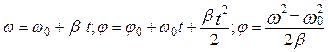 . (1.2.9)
. (1.2.9)
Рівноприскорений обертальний рух характеризується дотичним й нормальним або доцентровим прискореннями:
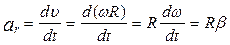 ;
;
у векторній формі 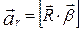 ,
,
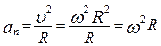 . (1.2.10)
. (1.2.10)
Зв’язок пройденого шляху по дузі кола з кутом повороту визначається так:
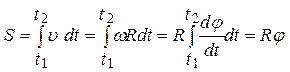 . (1.2.11)
. (1.2.11)
1.3. Тангенціальне й нормальне прискорення. Зв’язок між кінематичними величинами криволінійного руху
Розглянемо нерівномірний криволінійний рух матеріальної точки. За малий проміжок часу Dt лінійна швидкість точки змінюється від 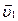 до
до 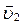 у відповідності з рисунком.
у відповідності з рисунком.
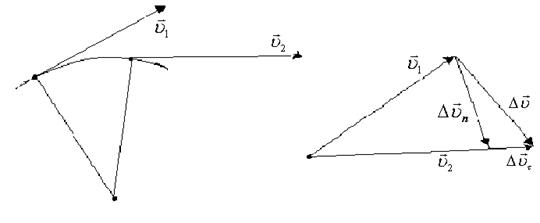
Рис.1.4
Вектори лінійної швидкості 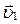 і
і 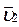 змінюється як за величиною, так і за напрямком. З рис.1.4. видно, що
змінюється як за величиною, так і за напрямком. З рис.1.4. видно, що
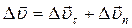 . (1.3.1)
. (1.3.1)
У цьому випадку миттєве прискорення точки буде дорівнювати
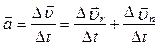 . (1.3.2)
. (1.3.2)
В граничному випадку при Dt®0, 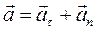 , де
, де
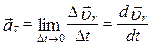
і
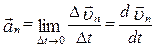 . (1.3.3)
. (1.3.3)
У випадку, коли вектори 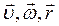 змінюються з часом, зв’язок між кінематичними величинами знаходять шляхом диференціювання за часом векторного добутку
змінюються з часом, зв’язок між кінематичними величинами знаходять шляхом диференціювання за часом векторного добутку 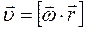 , тобто
, тобто
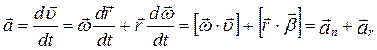 . (1.3.4)
. (1.3.4)
З цього співвідношення отримуємо:
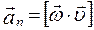
і
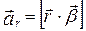 . (1.3.5)
. (1.3.5)
Напрямки векторів 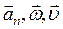 а також
а також 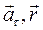 і
і 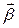 є взаємно перпендикулярними.
є взаємно перпендикулярними.
Із цих міркувань можна зробити такі висновки:
- нормальне й тангенціальне прискорення точки зростають лінійно із зростанням відстані точки до осі обертання;
- вектор дотичного або тангенціального прискорення завжди збігається з дотичною до колової траєкторії;
- вектор нормального прискорення направлений від точки на коловій траєкторії в стророну центра кола.
ЛЕКЦІЯ 2
Динаміка поступального руху точки
Дата добавления: 2015-08-26; просмотров: 886;
