Закон складання швидкостей
Розглянемо деякий процес, який відбувається у точці А, нерухомій відносно штрихованої системи координат. Позначимо тривалість деякого процесу за годинниками не штрихованої системи й штрихованої системи відповідно через t і tо. Очевидно, що
 ; і t = t2 – t1. (5.2.1)
; і t = t2 – t1. (5.2.1)
Для знаходження залежності tо від t скористаємось перетвореннями координат Лоренца (5.1.7)
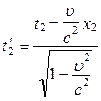 ;
; 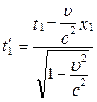 . (5.2.2)
. (5.2.2)
Віднімемо рівності (5.2.2), одержимо t0:
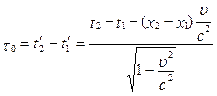 , але t2 - t1 =t , а x2 – x1 = ut,
, але t2 - t1 =t , а x2 – x1 = ut,
тому
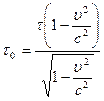 =
= 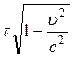 . (5.2.3)
. (5.2.3)
З рівності (5.2.3) знайдемо t
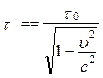 . (5.2.4)
. (5.2.4)
Висновок.
Якщо v»c, то t0<<t. Час в різних системах відліку протікає не однаково. Одна і та ж подія має різну тривалість у різних системах відліку.
Знайдемо довжину рухомого предмета в різних системах відліку. Нехай стрижень, який має довжину l0 в штрихованій системі координат, рухається разом з цією системою координат з швидкістю u відносно не штрихованої системи координат (рис. 5.2). (Стрижень перебуває у спокої відносно штрихованої системи координат).
Як видно з рисунка, довжина стрижня у штриховій системі координат дорівнює:
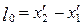 . (5.2.5)
. (5.2.5)

Рис. 5.2
Координати 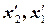 запишемо з перетворень Лоренца для моменту часу t (в один і той же час)
запишемо з перетворень Лоренца для моменту часу t (в один і той же час)
 .
.
Звідки
 . (5.2.6)
. (5.2.6)
Дата добавления: 2015-08-26; просмотров: 664;
