Кореляційний аналіз, регресійний аналіз.

Кореляційна залежність – це така залежність між величинами, що кожному значенню однієї випадкової величини відповідає певний закон розподілу іншої величини. Умовна щільність імовірності величини Y (f(Y/x)) – це щільність імовірності величини Y при зазначеному значенні величини Х. Якщо існують умовні щільності ймовірності величин Y (f(Y/x)) і X ( 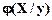), то говорять, що між величинами Y і Х існує кореляційна залежність.

Якщо щільність імовірності випадкової величини Y залежить від значення випадкової величини Х, те й математичне очікування величини Y залежить від цього значення, і можна говорити про умовне математичне очікування випадкової величини Y при заданому значенні величини Х (M(Y/x)). Таким чином, умовне математичне очікування величини Y є функцією величини Х, що математично можна записати так 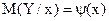, де функція 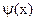називається функцією регресії Y на Х. Графік цієї функції називається лінією регресії. Якщо у вираженні для 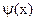присутні які-небудь постійні коефіцієнти, то вони називаються коефіцієнтами регресії. Аналогічно може бути уведене поняття функції регресії Х на Y. Якщо 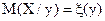, то функція 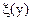- це функція регресії Х на Y, причому в більшості випадків лінії регресії Y на Х и Х на Y – це різні лінії.

Нехай є вибірка з n елементів, для кожного з яких визначаються значення випадкових величин Y й X, причому передбачається, що між цими величинами є кореляційна залежність. Якщо точки з координатами y_i й x_i (i = 1, 2,…, n) нанести на координатну площину XOY, те вийде так називане кореляційне поле. Виходячи з експериментальних даних, знаходять вибіркову оцінку коефіцієнта кореляції (вибірковий коефіцієнт кореляції), використовуючи формулу

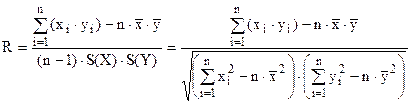, (1)

де R - вибірковий коефіцієнт кореляції.

Значення вибіркового коефіцієнта кореляції лежать в інтервалі 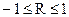. Якщо R > 0, то функції регресії Y на Х и Х на Y – це зростаючі функції, а якщо R < 0 – убутні. Чим ближче значення 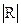до одиниці, тим тісніше точки кореляційного поля згруповані навколо прямій регресії, тобто тим більше підстав уважати функцію регресії лінійної. У цьому випадку говорять про сильну кореляційну залежність. Чим ближче значення R до нуля, тим гірше точки кореляційного поля лягають на пряму, і тем менше підстав уважати функцію регресії лінійної. Разом з тим, малі по модулі значення коефіцієнта кореляції зовсім не обов'язково означають відсутність кореляційної залежності між величинами Y і Х, вони лише означають, що немає достатніх підстав уважати цю залежність лінійної. Таким чином, коефіцієнт кореляції є мірою ступеня лінійності залежності між випадковими величинами, але не мірою ступеня залежності між цими величинами взагалі.

При визначенні функції регресії прийнято вважати оптимальними ті оцінки коефіцієнтів регресії, які отримані на основі застосування методу найменших квадратів.

Суть методу найменших квадратів полягає в тім, що оптимальним значенням коефіцієнтів регресії для функції 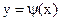, уважаються ті, для яких сума

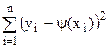приймає найменше значення.

В окремому випадку лінійної регресії виду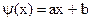

значення коефіцієнтів a й b визначають, мінімізуючи суму 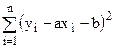. (2)

Для цього знаходять частки похідні вираження (2) по a і по b, дорівнюють ці похідні до нуля й вирішують систему, що виходить, рівнянь. У підсумку для оптимальних вибіркових оцінок коефіцієнтів регресії a й b одержують наступні вираження

; .

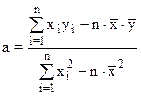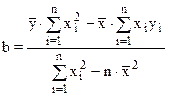З урахуванням виразу (1) останні вирази можуть бути перетворені до вигляду

; .

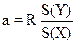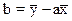У випадку регресії Х на Y функція регресії має вигляд

,

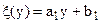а коефіцієнти регресії a₁ й b₁ обчислюються по формулах

; .

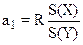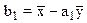Відзначимо, що лінії регресії Y на Х и Х на Y збігаються тільки в тому випадку, якщо 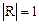. У цьому випадку між величинами Y і Х є лінійна функціональна залежність.

Лекція № 10. МЕДИЧНІ ПРИЛАДО-КОМП’ЮТЕРНІ СИСТЕМИ (МПКС)