Кореляційно-регресійний аналіз

Сучасна наука виходить із взаємозв'язку всіх явищ природи та суспільства.

Розрізняють 2 типи зв'язків між різними явищами і їхніми ознаками: функціональний (жорстко детермінований) і статистичний (стахостично детермінований) зв'язок.

Якщо зі зміною значення однієї з перемінних друга змінюється строго певним чином, тобто значенню однієї перемінної відповідає одне точно задане значення іншої перемінної, - то зв'язок між ними є функціональним.

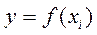(наприклад, 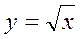) - функціональний зв'язок.

Стохастично детермінований зв'язок не має обмежень і умов, властивих функціональним зв'язкам.

Якщо зі зміною значення однієї з перемінних друга приймає у визначених межах будь-яке значення, то зв'язок називається стохастичним, тобто при різних значеннях однієї перемінної існують відповідні різні значення іншої перемінної.

Модель стохастичного зв'язку:

,

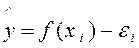де f ( x_i ) - частина результативної ознаки, що сформувалася під впливом врахованих, відомих факторних ознак (одного чи безлічі).

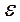_i - частина результативної ознаки, що виникла як слідство дії неконтрольованих, неврахованих факторів.

Кореляційним зв'язком називають найважливіший окремий випадок стохастической зв'язку, що складається в тому, що різним значенням однієї перемінної відповідають різні середні значення іншої.

Кореляційний зв'язок між ознаками може виникати різними шляхами:

1) Причинна залежність результативної ознаки від варіації факторної ознаки.

2) Зовсім інша інтерпретація необхідна для вивчення кореляційного зв'язку між двома наслідками загальної причини.

3) Виникнення кореляції: взаємозв'язок ознак, кожна з яких є і причина і наслідок.

Оскільки кореляційний зв'язок є статистичним, першою умовою можливості її вивчення є наявність даних по досить великій сукупності явищ.

Головною характеристикою кореляційного зв'язку є вивчення лінії регресії.

Теоретичною лінією регресії називається та лінія, навколо якої групуються крапки кореляційного поля, і яка вказує основний напрямок, тенденцію. Ця лінія повинна бути проведена так, щоб сума відхилень крапок поля кореляції від відповідних крапок теоретичної лінії регресії, дорівнювала нулю, а сума квадратів цих відхилень була б мінімальною.

Кореляційно-регресійний аналіз (КРА) складається з наступних етапів:

1) вибір форми регресії;

2) визначення параметрів рівня;

3) оцінка тісноти зв'язку;

4) перевірка адекватності моделі рівняння.

Найбільш часто використовуються для характеристики економічних показників наступні типи функцій:

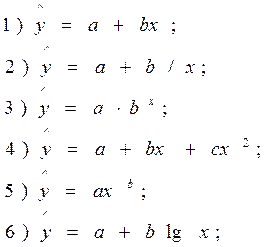
Найбільш часто застосовується в статистичному аналізі - лінійна функція:

Y = a + bx,

де а - вільний член рівняння;

b - коефіцієнт регресії, що показує на скільки одиниць у середньому змінюється величина результативної ознаки U при зміні факторної ознаки х на одиницю.

Визначення параметрів рівняння регресії виконується методом найменших квадратів, основною умовою якого є мінімізація суми квадратів відхилень емпіричних значень від теоретичних.

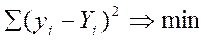
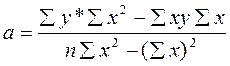
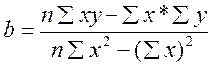
Дисперсію теоретичних значень називають факторною й обчислюють по формулі:

Факторна дисперсія:

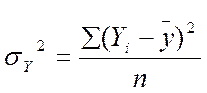
Замість середньої з внутрішньогрупової дисперсії обчислюють залишкову (випадкову) дисперсію.

Залишкова дисперсія:

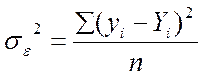
Загальна дисперсія:

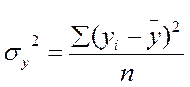
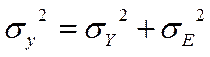
Мірою тісноти зв'язку є коефіцієнт детермінації:

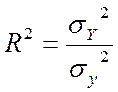
Тісноту зв'язку характеризує індекс кореляції:

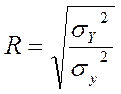
Кореляційно-регресійний аналіз може проводитися в умовах малої вибірки, тобто для обмеженого обсягу сукупності.

Щоб перевірити, наскільки ці показники характерні для всієї генеральної сукупності і чи не є вони результатом збігу випадкових обставин, необхідно перевірити адекватність статистичних спостережень. При чисельності об'єктів аналізу до 30, виникає необхідність перевірки значимості кожного коефіцієнту регресії.

Значимість коефіцієнту простої лінійної регресії визначається за допомогою критерію Фішера (F).

,

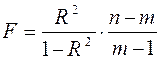де m – число параметрів в рівнянні регресії (=2);

n – обсяг сукупності (кількість досліджень =10).

Параметр визнається значимим за умови, якщо t_розр. > t_табл. (табличне значення див. у додатку).