Штучна нейронна мережа
КП
u0
| Дx | ВМ | Дy | ||

u
ОК
| x | y |
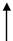 e
e
Рис. 1.2. Структура систем керування:
КП – керувальний пристрій; ВМ – виконавчий механізм; ОК – об’єкт керування; x –стан середовища; y –стан ОК; e –неспостережувані збурення; u0 –керувальнийсигнал; u – керувальний вплив; Дx і Дy – датчики стану середовища і об’єкта керування відповідно
Для цілеспрямованого функціонування керуювального пристрою йому, окрім інформації з датчиків Дx і Дy, потрібно також задати мету керування, яка надходить з тактичного рівня, і алгоритм керування, тобто спосіб досягнення заданої мети.
1.2. Труднощі побудови систем керування
Труднощі побудови СК визначаються складністю ОК. Наведемо основні ознаки складного ОК.
Брак математичного опису.Немає алгоритму обчислення стану y об’єкта за спостереженнями його входів(керованого u і некеровано-го) та спостережуваного стану середовища x.
Недетермінованість (стохастичність).Зумовлена переважноскладністю об’єкта і пов’язаними з цим численними другорядними процесами, якими нехтують під час побудови математичної моделі.
Нестаціонарність. Виявляється у дрейфі характеристик об’єкта.
1.3. Показники якості керування
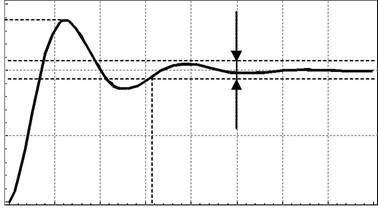
Якість керування, що забезпечується системами регулювання, ви-значається поведінкою системи як в усталеному режимі, так і під час перехідного процесу (див. рис. 1.3).
Основні показники перехідного процесу:
Перерегулювання
у = y max − y0 ⋅100,
 y0
y0
де σ вимірюють у відсотках.
Тривалість перехідного процесу T0–час з моменту виникненнястрибка задавального впливу, після якого відхилення регульованої ве-личини не перевищує заданого припустимого значення ∆e (рис. 1.3).
| y | |||
| ymax | 2∆e | ||
| y0 | |||
| T0 | t | ||
| Рис. 1.3. Характеристики перехідного процесу |
Якість керування в усталеному режимі визначається інтегральними оцінками, які дають змогу характеризувати перехідний процес у системі одним числом. На практиці найбільшого поширення набули такі інтегральні оцінки.
Квадратична інтегральна оцінка:
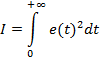
де e(t)=x(t)-y(t)
Поліпшена квадратична інтегральна оцінка:
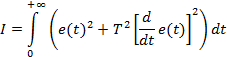
Перша із вказаних квадратичних оцінок тим менша, чим перехідний процес в розглядуваній системі ближчий до задавального впливу, а друга – чим він ближчий до перехідного процесу на виході інерційної ланки зі сталою часу T.
1.4. Типові математичні моделі об’єктів керування
На практиці точна модель ОК зазвичай невідома. Водночас для оцінних розрахунків корисно мати модель, що хоча б наближено опи-сувала властивості об’єкта.
Досвід показує, що в першому наближенні математичний опис бага-тьох промислових об’єктів, наприклад електричних та електромеханіч-них, можна подати у вигляді структури – моделі Гаммерштейна (рис. 1.4).
| u(t) | f(t) | y(t) | |||
| НЕ | ЛДЛ | ||||



Рис. 1.4. Типова структура об’єкта керування:
НЕ – безінерційний нелінійний елемент; ЛДЛ – лінійна динамічна ланка
Під НЕ розуміють нелінійність типу «зона нечутливості з обме-
женням» (рис. 1.5).
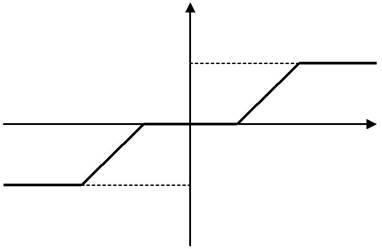
f f0
–u0
u0 u
–f0
Рис. 1.5. Характеристика нелінійного елемента
Передатна функція ЛДЛ зазвичай має вигляд
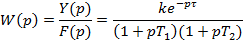
де F(p) і Y(p) – зображення за Лапласом (за нульових початкових умов) вхідного та вихідного сигналів ЛДЛ відповідно для об’єктів із самовирівнюванням

та для об’єктів без самовирівнювання.
1.5. Традиційні лінійні регулятори
Розглянемо замкнену (зі зворотним зв’язком) одноконтурну сис-тему автоматичного регулювання (рис. 1.6).
| x(t) | e(t) | Регулятор | u(t) | ОК | y(t) | |

Рис. 1.6. Структура системи автоматичного регулювання
Лінійні регулятори являють собою динамічні ланки, що описані лінійними диференціальними рівняннями. Найпоширенішими лінійними регуляторами є ПІД-регулятори, які мають такий математичний опис:
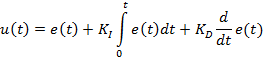
де u(t) – вихідний сигнал регулятора; e(t) – його вхідний сигнал (похибка регулювання); KP, KI, KD – коефіцієнти пропорційної, інтегральної та диференціальної складових відповідно.
Нехай ОК описано лінійною ланкою з передатною функцією (1.1), параметри об’єкта сталі, при цьому параметр τ досить малий. Передатна функція замкненої системи має відповідати передатній фу-
нкції ланки запізнювання зі сталою τ. При цьому регулятор буде опи-сано рівнянням (1.2) з такими параметрами:
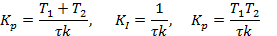
Зауважимо, що системи з ПІД-регуляторами перевершують за своїми характеристиками системи з ПІ-регуляторами, однак ПІ-регулятори менш чутливі до зміни параметрів об’єкта і простіше настроюванні.
1.6. Інтелектуальні системи керування
Інтелектуальні СК – це СК, здатні до «розуміння» і навчання щодо ОК, збурень, зовнішнього середовища та умов роботи.
Основна відмінність інтелектуальних систем полягає в наявності механізму системного оброблення знань.Головна архітектурна особ-
ливість, яка відрізняє інтелектуальні СК від традиційних, – це меха-
нізм отримання, зберігання і оброблення знань для реалізації функційкерування.
В основу створення інтелектуальних СК покладено два узагаль-нені принципи:
– керування на основі аналізу зовнішніх даних, ситуацій та подій (ситуаційне керування);
– використання сучасних інформаційних технологій оброблення знань.
Розрізняють декілька сучасних інформаційних технологій, що до-зволяють створювати інтелектуальні СК:
– експертні системи;
– штучні нейронні мережі (artificial neural networks);
– нечітка логіка (fuzzy logic);
– еволюційні методи і генетичні алгоритми (genetic algorithms).
В основу концепції інтелектуальності покладено:
– уміння працювати з формалізованими знаннями людини (екс-пертні системи, нечітка логіка);
– властиві людині способи навчання і мислення (нейронні мере-жі, генетичні алгоритми).
Структурно інтелектуальні СК містять додаткові блоки, які вико-нують системне опрацювання знань на основі цих інформаційних технологій. Такі блоки можна виконувати або як надбудову над зви-чайним регулятором, налагоджуючи належним чином його парамет-ри, або безпосередньо включатися у контур керування.
1.7. Застосування інтелектуальних систем керування
Найбільш суттєві причини поширення інтелектуальних СК такі:
– особливі якості інтелектуальних СК, зокрема мала чутливість до зміни параметрів ОК;
– те, що синтез інтелектуальної СК із застосуванням сучасних засобів апаратної та програмної підтримки часто простіший, ніж традиційних.
Є випадки, коли застосування інтелектуальних СК виправдане і дає кращий результат:
– системи регулювання, для яких модель ОК визначена лише якісно або її немає взагалі;
– як надбудова над традиційними системами для надання їм адап-тивних властивостей;
– відтворення дій людини-оператора;
– системи організаційного керування верхніх (стратегічного і тактичного) рівнів.
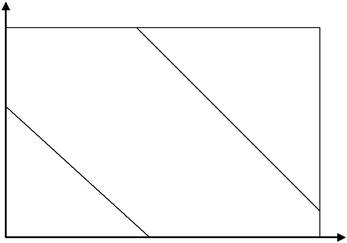
Сфера ефективного застосування традиційних, нейромережевих та нечітких СК щодо ОК, показані на рис. 1.7.
Застосування гібридного підходу (поєднання традиційних методів керування, нечіткої логіки та нейронних мереж) дозволяє створювати СК, ефективні в усьому спектрі ситуацій, і тому межі різних підходів, показаних на рис. 1.7, вельми умовні.
Немає
НМ
| Інформація | НЛ | |
| про ОК | ||
| ТМ | ||
| Повна |
Мала Складність ОКВелика
Рис. 1.7. Сфера ефективного застосування різних систем керування:ТМ – системи, які використовують традиційні методи керування; НЛ – системи керування з нечіткою логікою; НМ – системи керування на нейронних мережах
2. ГЕНЕТИЧНІ АЛГОРИТМИ
2.1. Вступ та історична довідка
Поширення та популярності генетичні алгоритми (ГА) набули завдяки роботам Дж. Холланда на початку 70-х років минулого століття. Однак генетичними вони стали називатися пізніше, а 1975 року Хол-ланд називав їх репродуктивними планами (reproductive plan).
Генетичні алгоритми базуються на теоретичних досягненнях синтетичної теорії еволюції, що враховує мікробіологічні механізми успадковування ознак у природних і штучних популяціях організмів, а також на нагромадженому людському досвіді у селекції тварин і рослин.
Методологія ГА ґрунтується на гіпотезі селекції, яка у загальному вигляді може бути визначена так: чим вища пристосованість особини, тим вища ймовірність того, що у потомстві, отриманому за її участі, ознаки, що визначають пристосованість, будуть виражені ще сильніше.
Попри свою біологічну термінологію, ГА перш за все – це потужний засіб розв’язування задач глобальної оптимізації. Інакше кажучи, ГА переважно застосовують для знаходження глобальних екстремумів функцій багатьох змінних. Від інших методів оптимізації ГА відрізняються таким:
– колективним пошуком екстремуму за допомогою популяції особин;
– обробляють не значення параметрів самої задачі, а їх закодовану форму;
– використовують тільки цільову функцію, а не її похідні чи будь-яку іншу додаткову інформацію;
– застосовують імовірнісні, а не детерміновані правила вибору і модифікації параметрів задачі.
Розглянемо ці аспекти детальніше.
2.2. Подання параметрів оптимізації
Нехай маємо деяку цільову функцію багатьох змінних f(x1, x2, …, xn),для якої потрібно знайти глобальний екстремум(мінімум або максимум). Подамо незалежні змінні у вигляді ланцюжка двійкових чисел 1 і 0 (ланцюжка бітів), виділяючи для кожного параметра m бітів
(рис. 2.1).
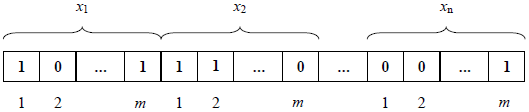
Рис. 2.1. Структура«хромосоми»
Такий ланцюжок бітів, що кодує параметри оптимізації, називають хромосомою, а окремі біти в ній – генами.
Хромосоми генеруються випадково, послідовним заповненням розрядів (генів), одразу в двійковому вигляді, і всі подальші зміни в популяції зачіпають спочатку генетичний рівень, а тільки потім наслідки цих змін аналізують у параметрах оптимізації, і ніколи навпаки.
У принципі, для декодування генетичної інформації із двійкової форми до десяткової підходить будь-який двійково-десятковий код, але найкращі результати забезпечує подання хромосом із використанням коду Грея (див. табл. 2.1).
Таблиця 2.1
Декодування параметрів із різних двійкових кодів
| Код Грея | Двійковий код | Десяткове значення |
Продовження таблиці 2.1
| Код Грея | Двійковий код | Десяткове значення | |
Від коду Грея переходимо до двійково-десяткового коду, а від нього – до натуральних цілих чисел. Відношення отриманого числа до максимального числа, доступного для кодування такою кількістю розрядів (в табл. 2.1 це число 15) і дає шукане значення зсуву змінної відносно лівої межі аі допустимого діапазону її зміни, нормованого на ширину діапазону:
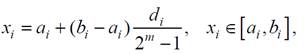
де di – ціле десяткове число, отримане переведенням коду з двійкового в десяткове подання; ai – нижня межа допустимих значень для параметра xi , а bi – його верхня межа.
На відміну від звичайного двійково-десяткового подання код Грея гарантує, що дві сусідні вершини гіперкуба, на якому здійснюється пошук, котрі належать одному ребру, завжди декодуються в дві найближчі точки простору дійсних чисел, розміщених на відстані в одну величину точності їх дискретного подання.
17
Альтернативою двійковому кодуванню можна вважати метод логарифмічного кодування,який застосовується для зменшення довжини хромосоми. Його використовують здебільшого в задачах багатовимірної оптимізації з великими просторами пошуку розв’язків.
Під час логарифмічного кодування перший біт ( α) закодованої послідовності – це біт знака показникової функції, другий біт (β ) – біт знака степеня цієї функції, а решта бітів (bin) – це значення самого степеня:

де [ bin]10 – десяткове значення числа, закодованого у вигляді двійкової послідовності bin.
2.3. Генетичні оператори
У процесі функціонування ГА хромосоми зазнають трьох основних видів модифікації (операторів): схрещування (cross-over), мутації (mutation) та інверсії (inversion).
Схрещування.Під час схрещування в двох обраних хромосомахвипадково обирається точка схрещування і потім відбувається обмін частин хромосом-батьків з утворенням двох нащадків (рис. 2.2).
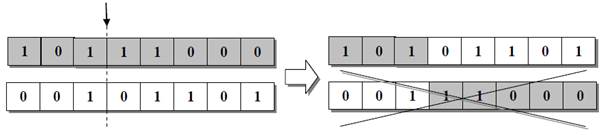
Рис. 2.2. Дія оператора схрещування
Далі з двох утворених нащадків випадково обирається тільки один. Усі генетичні оператори застосовуються із заздалегідь вибраною імовірністю (в діапазоні від 0 до 1). Типова ймовірність застосування оператора схрещування на якому здійснюється пошук – 0,9.
Мутація. У процесі мутації випадково обраний ген змінюється напротилежний (рис. 2.3). Типова ймовірність застосування мутації – 0,1. 
Рис. 2.3. Дія оператора мутації
Інверсія. Оператор інверсії змінює послідовність генів у хромосомі відносно випадково вибраної точки (рис. 2.4).

Рис. 2.4. Дія оператора інверсії
Зазвичай оператор інверсії застосовують з імовірністю 0,01.
Репродуктивний план Холланда
Основний (класичний) генетичний алгоритм, відомий також як репродуктивний план Холланда, складається з таких кроків:
Крок 1.Ініціалізація–формування початкової популяції(наборухромосом, множини потенційних розв’язків) випадковим чином.
Крок 2.Оцінювання пристосованості–розрахунок функцій пристосованості для кожної особини (хромосоми) в популяції.
Крок 3.Перевірка умови зупинення алгоритму–зупиненняалгоритму після досягнення очікуваного оптимального значення, можливо із заданою точністю (залежно від його конкретного застосування).
Крок 4.Селекція хромосом–вибір за розрахованими значеннямифункції пристосованості тих хромосом, які будуть брати участь у створенні нащадків для наступного покоління популяції.
19
Крок 5.Застосування операторів–застосування генетичних операторів схрещування, мутації та інверсій до вибраних на попередньому кроці батьківських хромосом.
Крок 6.Створення нового покоління–циклічне повторення кроків 4 і 5, доки популяція наступного покоління не заповниться вся.
Крок 7.Вибір найкращої хромосоми–обрання розв’язком задачіхромосоми з найкращим значенням функції пристосованості, коли умова зупинення еволюції виконана.
Блок-схему репродуктивного плану Холланда показано на рис. 2.5. Розглянемо тепер докладніше найбільш значущі елементи наведеного алгоритму.
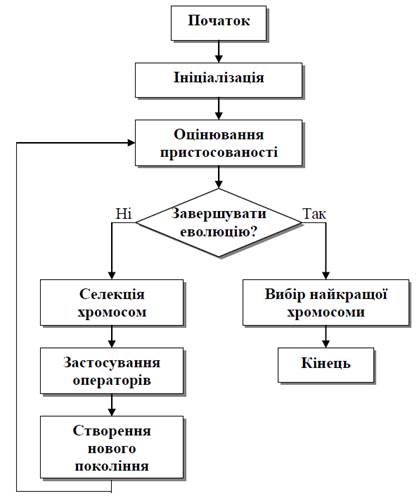 |
Рис. 2.5. Блок-схема генетичного алгоритму
2.5. Функція пристосованості
Оцінювання пристосованості хромосом у популяції полягає в роз-раховування функції пристосованості (fitness function). Чим більше зна-чення цієї функції, тим вища «якість» хромосоми, а отже, і відповідного їй розв’язку задачі. Форма функції пристосованості залежить від харак-теру розв’язуваної задачі. Припустимо, що для розв’язання вихідної за-дачі треба максимізувати цю функцію. Якщо вихідна форма функції пристосованості не задовольняє цих умов, то виконують відповідне пе-ретворення. Наприклад, задачу мінімізації функції можна легко звести до задачі максимізації оберненням цільової функції.
Аргументами для функції пристосованості стають значення па-раметрів оптимізації, отримані з певної хромосоми декодуванням.
2.6. Селекція батьківських хромосом
За розрахованими значеннями функції пристосованості з поточ-ної популяції вибираються батьківські хромосоми для подальшого схрещування, продукування нащадків і формування нового поколін-ня. Такий вибір роблять відповідно до принципу природного добору, за яким найбільші шанси на участь у створенні нових особин мають хромосоми з найбільшими значеннями функції пристосованості.
Є різні методи селекції. Найбільш популярним вважається метод рулетки (roulette wheel selection),який свою назву отримав за аналогі-єю з відомою азартною грою. Кожній хромосомі відповідатиме сектор колеса рулетки, розмір якого задають пропорційним значенню функ-ції пристосованості цієї хромосоми:
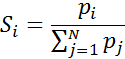
де Si – розмір «сектора»; N – кількість хромосом (особин) у популяції; pi –нормоване за такою формулою значення функції пристосованості.
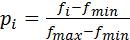 (2.1)
(2.1)
де fi – ненормоване значення, отримане в результаті обчислення фу-нкції пристосованості; fmin і fmax – відповідно мінімальне і максимальне значення функції пристосованості посеред її значень, обчислених для всіх хромосом у популяції.
Тож, чим більше значення функції пристосованості, тим більший сектор на колесі рулетки. Як видно з виразу (2.1) сума величин усіх секторів дорівнює одиниці (рис. 2.6).
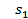
| 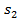
| 
| … | 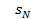
| |||||||
| Випадкове число від 0 до 1 |



Рис. 2.6. Розподіл«секторів рулетки»в діапазоні від0до1(... < s2 < sN < s1 < s3 < ...)
Після цього генерується випадкове число в діапазоні від 0 до 1 і перевіряється, в який сектор воно потрапило. «Успішна» хромосома (на рис. 2.6 – це хромосома 3) і вибирається як батьківська для формування наступного покоління.
Слід зазначити, що у деяких модифікаціях ГА процес вибору батьківських хромосом не завжди випадковий. Зокрема, за підходу, котрий називають елітизм або елітарна стратегія, одна або декілька хромосом з найвищим значенням функції пристосованості одразу переносяться в наступне покоління без жодних модифікацій, тобто без застосування генетичних операторів.
2.7. Критерії зупинення еволюції
Визначення умови зупинення ГА залежить від його конкретного застосування. В оптимізаційних задачах, якщо відоме максимальне (або мінімальне) значення функції пристосованості, то зупинення
алгоритму може відбутися після досягнення очікуваного оптимального значення заданої точності. Алгоритм може також зупинятися у випадку, коли його виконання не сприяє поліпшенню вже досягнутого значення. Алгоритм може бути зупинено після закінчення визначеного часу виконання або після виконання заданої кількості операцій.
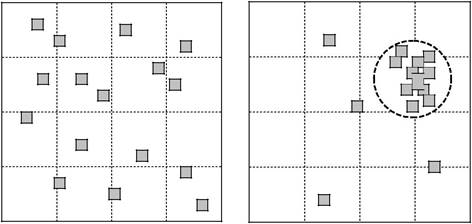
Окрім цього, критерієм зупинення може бути факт попадання певної кількості хромосом популяції у наперед заданий окіл їх усередненого значення. У процесі еволюції (ітерацій алгоритму) дедалі більше хромосом набуває ознак оптимального розв’язку задачі, що означає деяку їх «схожість». Це означає, що щільність хромосом в околі оптимуму буде збільшуватись (рис. 2.7).
На початку еволюції У кінці еволюції
| x2 | x2 | |
x1 x1
Рис. 2.7. Зміна стану популяції в процесі еволюції
Оцінюючи радіус розкиду параметрів від їх середнього значення, можна зупинити алгоритм, коли цей радіус стане достатньо малим. Середнє значення за кожним з параметрів оптимізації розраховують як

де N – кількість хромосом у популяції; xij – значення (після декодування)
j-го параметра в i-й хромосомі.
Тоді відстань від i хромосоми до центру буде
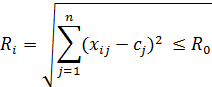
Коли відстань (2.2) стане меншою від прийнятого R0 для наперед заданої кількості хромосом, алгоритм зупиняється.
2.8. Генетичні алгоритми для багатокритерійної оптимізації
Більшість задач, які розв’язують за допомогою генетичних алгоритмів, мають один критерій оптимізації, який використовують як функцію пристосованості. У свою чергу, багатокритерійна оптимізація ґрунтується на відшукуванні розв’язку, що одночасно оптимізує більше, ніж одну функцію. В цьому випадку шукають певний компроміс, яким і виступає розв’язок.
Є декілька класичних методів, що стосуються багатокритерійної оптимізації. Один з них – це метод зваженої функції (method of objective weighting).Відповідно до цього методу функції fi,що оптимізуються, взяті із вагами wi, утворюють єдину функцію:
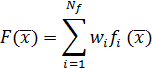
де Nf – кількість функцій, що оптимізуються 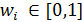 і
і
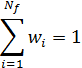
Ще один підхід до багатокритерійної оптимізації пов’язаний із розділенням популяції на підгрупи однакового розміру (sub-populations),кожна з яких«відповідає»за одну функцію,яку оптимі-зують. Селекцію виконують автономно для кожної функції, однак операцію схрещування виконують без урахування меж підгруп.
3. БІОЛОГІЧНІ ТА ШТУЧНІ НЕЙРОННІ МЕРЕЖІ
3.1. Біологічний нейрон
Попри розбіжності у будові, всі нейрони проводять інформацію однаково. Нейрони отримують сигнали сильно розгалуженими відростками (дендритами), а посилають сигнали по нерозгалуженим відросткам (аксонам). Інформація передається по аксонах (рис. 3.1) у вигляді коротких електричних імпульсів, так званих потенціалів дії, амплітуда яких становить приблизно 100 мВ, а тривалість – 1 мс.
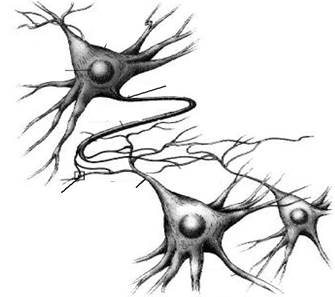
Ядро
Аксон
Синапс Дендрит
Рис. 3.1. Нервові клітини головного мозку людини
Але не будь-який імпульс, що надійшов у нейрон по дендритах, передається на аксон. Лише за досягнення певного критичного (порогового) значення потенціалу, клітина генерує сигнал, що проходить по аксону до інших нейронів. Швидкість поширення нервового імпульсу по аксону досягає 100 м/с.
3.2. Історія штучних нейронних мереж
Здатність нейроподібних структур до навчання вперше дослідили Дж. Маккалок та У. Пітт. У 1943 році вийшла їх робота «Логічне чис
лення ідей, що стосуються нервової діяльності», в якій було описано модель нейрона і сформульовано принципи побудови штучних нейронних мереж (ШНМ).
Великий поштовх розвиткові нейрокібернетики дав американський нейрофізіолог Ф. Розенблат, який запропонував 1962 року свою модель нейронної мережі – персептрон. Сприйнятий спочатку з великим ентузіазмом, він невздовзі зазнав нищівної критики з боку великих наукових авторитетів. І хоча детальний аналіз їх аргументів показує, що вони заперечували не зовсім той персептрон, який пропонував Ф. Розенблат, дослідження ШНМ було згорнуто майже на 10 років. Попри це в 70-ті роки було запропоновано багато цікавих розробок, таких, наприклад, як когнітрон, здатний добре розпізнавати досить складні образи незалежно від повороту і зміни масштабу зображення.
У 1982 році американський біофізик Дж. Хопфілд запропонував оригінальну модель ШНМ, названу його іменем. За наступні декілька років було винайдено мережу зустрічного потоку, двонапрямлену асоціативну пам’ять та багато інших алгоритмів.
В інституті кібернетики ім. В. М. Глушкова НАН України з 70-х років ведуть роботу над стохастичними нейронними мережами.
Штучна нейронна мережа
Найбільш містке визначення ШНМ таке:
Штучна нейронна мережа – це суттєво паралельно розподілений процесор, здатний зберігати і відтворювати дослідне знання.
Вона схожа з мозком людини у двох аспектах:
– мережа набуває знань у процесі навчання;
– для збереження знань мережа використовує сили міжнейронних з’єднань (синаптичних ваг).
| ||||
| ||||
| ||||




x1 
x2
|
|
|





... 
xn 
Рис. 3.2. Схема штучного нейрона
Штучний нейрон, схему якого показано на рис. 3.2, працює так.
Сигнали xi (i =1,...,n) , що надходять на вхід нейрона, множаться на
вагові коефіцієнти wi (синаптичні ваги). Далі вони додаються і вислі-
дний сигнал зсувається на величину w0 порогового зсуву:
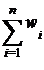 |
S = xi + w0 . (3.1)
Потім вихідний сигнал S подається на вхід блоку, що реалізує
нелінійну активаційну функцію нейрона h(S) .
3.4. Типи активаційних функцій
Традиційно активаційні функції східчасті, тобто сигнал на виході
нейрона з’являється тільки тоді, коли сумарний вхідний вплив пере-
вищує певне порогове значення.
Одна з умов реалізації якогось перетворення за допомогою ШНМ –
це нелінійність її активаційної функції. Для перетворень найчастіше
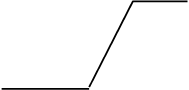
використовують такі функції: лінійні, лінійні з насиченням (рис. 3.3,
а, б); порогові функції (рис. 3.3, в, г); сигмоподібні тангенціальні фун-
кції (рис. 3.3, д); сигмоподібні логарифмічні (рис. 3.3, е); гармонічні
функції та радіально-базисні.
Хоча лінійна функція у чистому вигляді й не дозволяє реалізува-
ти будь-якого перетворення, проте вона часто може виявитись корис-
ною для простого масштабування вихідного сигналу нейрона.
|
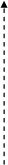
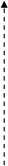
h



S
а
h




S
в

h





S
д
Рис. 3.3. Графіки активаційних функцій: а – лінійної з насиченням;
б – лінійної з насиченням (зміщеної); в – порогової; г – порогової (зміщеної);
д – сигмоподібної тангенціальної; е – сигмоподібної логарифмічної
Сигмоподібні функції найчастіше застосовують у нейронних ме-
режах. Їх описують такими функціональними залежностями:
| |
h(S) = -1 – тангенціальною; 
1+ e-x
h(S) = – логарифмічною. 
1+ e-x
Функції синуса або косинуса (гармонічні функції) досить часто
використовують у нейронних мережах для подання періодичних пе-
ретворень.
Радіально-базисна функція має такий вигляд: h(S) = e- x2 .
Наведені активаційні функції найбільш вживані, але в жодному
разі не перекривають усіх можливих.
Дата добавления: 2015-08-26; просмотров: 2670;
