ВЫПУКЛЫЕ ФУНКЦИИ И НЕКОТОРЫЕ ИХ СВОЙСТВА
Определение 1:
Функция многих переменных f(x), определенная на выпуклом множестве U 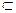 En, называется выпуклой функцией, если
En, называется выпуклой функцией, если
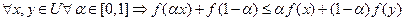 (1)
(1)
Геометрический смысл. Правую часть неравенства (1) можно переписать в виде: 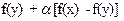 :
:
 f
f 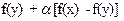
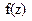
y z x x
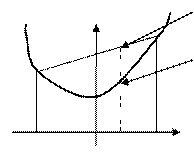
Таким образом, можно сказать, что функция выпуклая, если ее график лежит всегда ниже секущей между точками пересечения
Определение 2
Если в выражении (1) знак неравенства ≥, то такие функции называются вогнутыми
Вопрос: Существуют ли функции одновременно и выпуклые и вогнутые
Ответ: Существуют. Это линейная функция 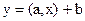
Утверждение:
Пусть f(x) дважды непрерывно дифференцируема на выпуклом множестве U 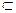 En , тогда, для того, чтобы она была выпуклой
En , тогда, для того, чтобы она была выпуклой  чтобы f"(x)>0
чтобы f"(x)>0 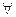 x
x 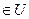
Теорема 1:
Пусть f(x) один раз непрерывно дифференцируема на выпуклом множестве U 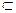 En , тогда, для того, чтобы она была выпуклой
En , тогда, для того, чтобы она была выпуклой 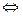 чтобы
чтобы 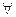 x,y
x,y 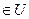 выполнялось
выполнялось 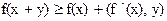 .
.
Доказательство:
Доказательство мы приведем при более жестком требовании: функция дважды непрерывно дифференцируема.
Тогда по теореме о среднем:
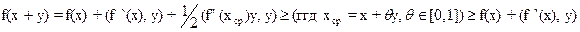
Ч.т.д.
Замечание: Значительно усложнив доказательство, можно избавиться от предположения о дважды непрерывной дифференцируемости.
Теорема 2:
Пусть функция 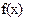 выпуклая и дифференцируемая в En , для того, чтобы функция достигала в точке
выпуклая и дифференцируемая в En , для того, чтобы функция достигала в точке 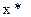 своего глобального минимума
своего глобального минимума 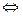 чтобы
чтобы 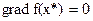 .
.
Доказательство:
1. Необходимость
Следует из теоремы о необходимом условии безусловного минимума
2. Достаточность
Пусть 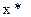 некоторая точка, в которой
некоторая точка, в которой 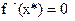 . Докажем, что
. Докажем, что 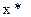 - глобальный минимум. Для этого воспользуемся предыдущей теоремой, полагая
- глобальный минимум. Для этого воспользуемся предыдущей теоремой, полагая  , тогда получим:
, тогда получим:
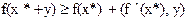
В силу предположения теоремы 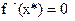 мы получаем:
мы получаем:
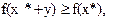 т.к. y произвольная, то
т.к. y произвольная, то 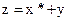 тоже произвольная
тоже произвольная
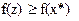
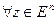
Ч.т.д.
Определение:
Задача 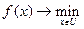 называется задачей выпуклого программирования, если функция
называется задачей выпуклого программирования, если функция 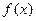 и множество U – выпуклые.
и множество U – выпуклые.
Если при этом U определено следующим образом:
U= {x 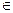 En:
En: 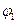 (x)≥0, ..
(x)≥0, .. 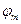 (x)≥0}, то мы имеем основную задачу выпуклого программирования
(x)≥0}, то мы имеем основную задачу выпуклого программирования
Определение:
Основная задача выпуклого программирования называется регулярной, если существует такая точка 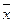 , для которой
, для которой 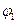 (
( 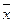 )≥0
)≥0 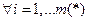 . Условие (*) называется условием регулярности Слейтера. Условие регулярности Слейтера означает, что U имеет внутренние точки.
. Условие (*) называется условием регулярности Слейтера. Условие регулярности Слейтера означает, что U имеет внутренние точки.
Из теоремы 2 (необходимого условия условного минимума) мы получаем необходимое условие для основной задачи выпуклого программирования:
Для того чтобы точка x* 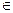 U была решением основной задачи выпуклого программирования необходимо, чтобы
U была решением основной задачи выпуклого программирования необходимо, чтобы 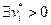 , что выполняется равенство:
, что выполняется равенство:
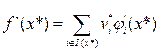 (2)
(2)
при этом предполагается, что градиенты активных ограничений л.н.з.
Ниже будет сформулировано необходимое условие так, чтобы не использовались градиенты целевой функции и градиенты ограничений.
1. Условие дополняющей нежесткости.
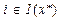
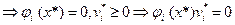
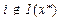
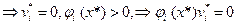
Таким образом, получаем, что 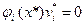
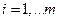 (3)
(3)
Условие (3) называется условием дополняющей нежесткости.
2. Функция Лагранжа
Введем в рассмотрение вектор 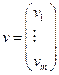 и функцию
и функцию 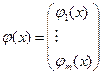 , тогда условие (3) можно записать в виде:
, тогда условие (3) можно записать в виде:
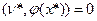 (4)
(4)
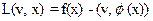 (5)
(5)
Emxn 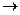 R
R
Такая функция (5) называется функцией Лагранжа выпуклого программирования.
f(x) - выпуклая
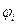 (x) – вогнутые (-
(x) – вогнутые (- 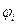 (x) –выпуклые)
(x) –выпуклые)
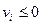 , то L(v, x)- выпуклая функция по х.
, то L(v, x)- выпуклая функция по х.
Рассмотрим
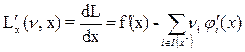
Возьмем точку 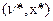 :
:
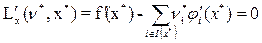 согласно равенству (2).
согласно равенству (2).
Таким образом, мы получили, что 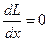 , откуда следует, что
, откуда следует, что 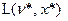 по х достигает своего условного минимума в точке
по х достигает своего условного минимума в точке 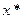 , а значит,
, а значит,
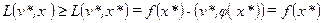
3. Покажем, что функция Лагранжа достигает по v 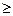 0 своего максимума, а именно:
0 своего максимума, а именно:
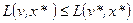
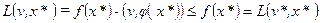
Определение:
Точка 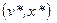 называется седловой точкой функции Лагранжа, если эта функция имеет минимум по x и максимум по v в этой точке.
называется седловой точкой функции Лагранжа, если эта функция имеет минимум по x и максимум по v в этой точке.
Необходимое условие минимума в основной задаче может быть сформулировано следующим образом:
Для того чтобы x* 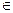 U была решением задачи выпуклого программирования необходимо, чтобы для v*
U была решением задачи выпуклого программирования необходимо, чтобы для v* 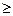 0 точка
0 точка 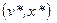 была седловой точкой, при этом предполагается , что {
была седловой точкой, при этом предполагается , что { 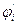 },
}, 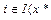 ) л.н.з.
) л.н.з.
Дата добавления: 2015-08-26; просмотров: 2117;
