ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ. Множество U En называется выпуклым множеством, если
Определение:
Множество U 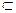 En называется выпуклым множеством, если
En называется выпуклым множеством, если 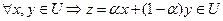
 Геометрический смысл:
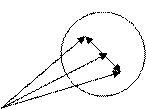
Геометрический смысл:
x
x-y U
z 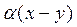
y
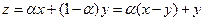
Таким образом, можно сказать, что U выпуклое, если наряду с любыми двумя своими точками содержит и весь отрезок, соединяющий эти точки.
Примеры:
1.) 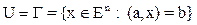 – гиперплоскость. Доказать, что множество U – выпуклое.
– гиперплоскость. Доказать, что множество U – выпуклое.
Доказательство:
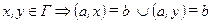 .
.
Возьмем 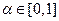 и докажем, что
и докажем, что 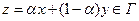 :
:
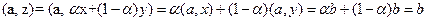
Ч.т.д.
2.) 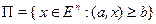 – полупространство. Доказать, что множество U – выпуклое.
– полупространство. Доказать, что множество U – выпуклое.
E2
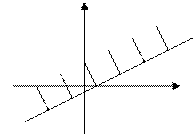 x2
x2
x1
Доказательство:
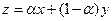
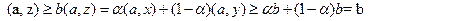 Ч.т.д.
Ч.т.д.
3.) U 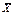 ,r ={ x
,r ={ x 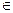 En: ||x-
En: ||x- 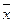 ||≤ r } шар в En . Доказать, что множество U – выпуклое.
||≤ r } шар в En . Доказать, что множество U – выпуклое.
Доказательство:
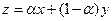
||z- 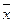 ||≤ r
||≤ r
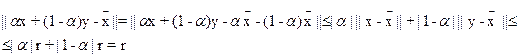
Ч.т.д.
12
Дата добавления: 2015-08-26; просмотров: 1179;
