Сила давления на цилиндрическую поверхность.

Представим трубу длиной l, с внутренним радиусом 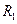и внешним радиусом 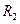(см. рис. 2.20). Толщина трубы e = 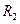– 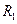. В трубе находится жидкость с давление. Внешнее давление – 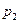. Необходимо установить минимальную толщину e, при которой труба не разорвется.

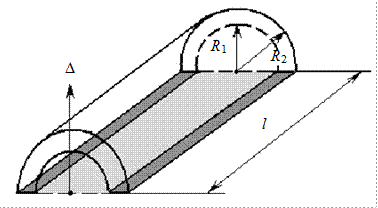
Рис. 2.20. Определение силы давления в цилиндрической трубе

Выберем направление Δ, совпадающее с одним из радиусов трубы.

Равнодействующая сил внутреннего давления

,

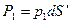где S' – проекция поверхности S на плоскость, перпендикулярную направлению Δ. Поверхность S' является прямоугольником, площадь которого 2 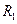l, тогда

.

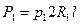Аналогичный результат можно получить для силы внешнего давления

.

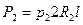Для второй части трубы мы получим тот же результат.

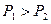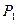Если внутреннее давление будет больше внешнего (сила будет стремиться разорвать трубу), направление Δ было выбрано произвольно, поэтому можно сделать вывод, что разрыв может произойти по любому направлению. Материал трубы в силу своих физических свойств будет сопротивляться разрыву. Это сопротивление будет тем больше, чем толще будет труба. Величина, характеризующая способность материала сопротивляться его разрыву обозначается σ. Сила сопротивления материала

,

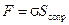где 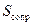– площадь сопротивления.

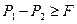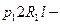
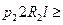
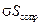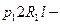
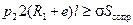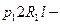
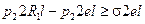Таким образом, разрыв произойдет в случае, если , или , или , или , или 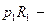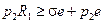, откуда следует, что при

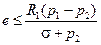
(2.19)

произойдет разрыв трубы.