Сила давления на криволинейную поверхность.

Рассмотрим поверхность S, на которую с внешней стороны воздействует жидкость, создавая давление 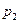, воздействие жидкости с внутренней стороны – (см. рис. 2.19). Каждый элемент поверхности площадью ds испытывает воздействие силы давления с внешней стороны

,

где 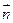– единичный вектор, направленный по нормали к ds, ориентированный в сторону внешней жидкости.

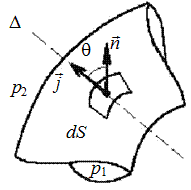
Рис. 2.19. Определение силы давления на криволинейную поверхность

Равнодействующая от суммы всех элементарных сил, действующих на поверхность изнутри :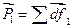

Эту силу трудно подсчитать, т.к. векторы 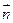не параллельны между собой.

Проекция силы 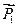, по направлению единичного вектора 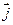будет

.

Если θ – угол между направлением Δ и нормалью к поверхности ds, то 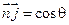, тогда

.

В то же время 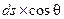= ds',тогда 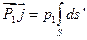, или , где dS' – проекция поверхности S на поверхность, перпендикулярную выбранному направлению Δ.

Таким образом, можно записать 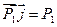, как произведение двух векторов и

.

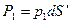(2.17)

Такой же результат мы получим для равнодействующей силы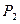

.

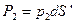(2.18)