Графическое счисление пути судна

Счисление координат судна (счислением) называется вычисление текущих координат судна от известных координат по времени, курсу и скорости с учетом влияния на судно ветра и течения. Графическое счисление выполняется непосредственно на морской навигационной карте с использованием штурманских прокладочных инструментов (параллельной линейки, транспортира и циркуля измерителя) и называется графическим счислением или навигационной прокладкой. Навигационная прокладка это графическое изображение на морской карте пройденного судном маршрута (или части его), выполненное автоматически или вручную на основе измерений и вычислений. Если счисление выполняется по формулам и таблицам, оно называется аналитическим (письменным). Прокладка может быть предварительной и исполнительной. Предварительной прокладкой называется навигационная прокладка маршрута судна, выполненная предварительно, исходя из намеченного маршрута, отвечающего требованиям плавания, поставленным задачам и экономической целесообразности. При выборе пути судна руководствуются двумя условиями:

1. безопасность плавания,

2. экономичность перехода (как правило, это наименьшая затрата времени).

Выбранный маршрут наносится на навигационные генеральные карты с указанием курсов, длительности пути на курсе и точек поворота или ориентиров в точках поворота. Дальнейшая задача судоводителя сводится к обеспечению движения судна по намеченному пути и контролю за этим движением (исполнительная прокладка). Навигационная прокладка начинается с момента выхода судна с акватории порта и заканчивается в момент прихода судна в порт (от причала до причала). Основным методом непрерывного учета положения судна является графическое счисление. Оно заключается в систематическом нанесении положения судна на карту по данным о его движении и пройденного расстояния, а также сведениям о течении и дрейфе. Начальная точка счисления должна быть известна. Место судна, координаты которого получены по счислению, называются счислимыми.

Контроль прокладки производится путем измерения различных навигационных параметров (пеленгов, расстояний, разности расстояний и высот светил) и получения места судна путем обсервации по двум, трем и более линиям положения.

Геометрические величины, измеряемые непосредственно или же получаемые косвенным путем для определения места судна в море по береговым и небесным светилам называются навигационными параметрами.

Геометрическое место точек, отвечающих постоянному значению величины, измеренной для обсервации (навигационного параметра) называется изолинией. Изолиния в общем случае является кривой линией. Для обсервации необходимо иметь лишь небольшие отрезки изолиний в точке пересечения их под углом друг к другу. Отрезки изолиний без особой погрешности можно заменить отрезками прямых, касательных к изолинии или их секущими. Касательная или секущая к изолинии называется линией положения. Изолиниями могут быть пеленг, изостадия (окружность), изогона (окружность), гипербола.

Все графические работы, выполняемые на карте, состоят из отдельных элементов задачи. К таким задачам относят снятие с карты координат судна или нанесения места судна на карту, расчет и прокладка курсов и пеленгов, измерение расстояний между определенными точками. При ведении прокладки решаются задачи двух типов: прямая и обратная.

Первая (прямая) задача предусматривает только учет движения судна, когда курс рулевому задан.

ИК = КК + Dк.

Рассчитывают истинный курс и прокладывают на карте линию курса в виде прямой от исходной точки. При отсутствии сноса от течения и ветра (дрейфа) линия истинного курса будет совпадать с путевым углом, следовательно, судно будет перемещаться по проложенному на карте курсу. На карте у точки, принятой за исходную для ведения счисления, надписывается время с точностью до 1 минуты и отсчет лага с точностью до 0,1 мили ( 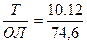). Дальнейшее нанесение положения судна на любой момент времени производится по расстоянию, пройденному судном по лагу от исходной точки. Положение судна на линии проложенного курса отмечается каждый час при плавании вблизи берегов и каждую вахту – при плавании в открытом море, а также при любом изменении курса или скорости. Каждую счислимую точку обозначают чертой длиной около 5 мм, перпендикулярной предшествующему курсу. Каждую обсервованную точку отмечают специальным знаком, присвоенным данному виду обсервации.

В практике судовождения обратная задача встречается гораздо чаще и состоит в том, что судну необходимо следовать заданным ИК. В этом случае рулевому задается предварительно рассчитанный КК, исходя из проложенного ИК.

КК = ИК - Dк.

Если необходимо рассчитать отсчет лага на момент прихода в заданную точку, то предварительно снимают с карты S – расстояние, которое необходимо пройти от исходной точки до точки поворота. Далее рассчитывают РОЛ и затем ОЛ₂.

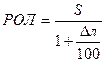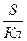= и ОЛ₂ = ОЛ₁ + РОЛ

Время прихода в расчетную точку рассчитывают:

T₂ = T₁ + DT = T₂ +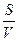

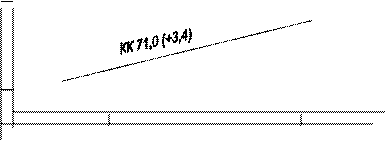
Вдоль линии курса надписывается компасный курс судна, в скобках - поправка компаса.

30¢

+

+

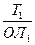
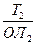
47°

04°00Е 04°20¢

Рис. 1.24

Прямая задача Обратная задача

КК – задан ИК – снят с карты

+(±)d - из таблицы девиации по КК -(±)d – с карты

МК – магнитный курс МК – магнитный курс

+(±)d – склонение с карты -(±)d - из табл. девиации по МК

ИК КК

При прямой задаче выбранные склонение и девиация со своим знаком складываются с КК и МК, а при обратной задаче – вычитаются из ИК и МК.

Учет дрейфа и постоянного течения при прокладке.

Дрейфом судна называется смещение движущегося судна с линии истинного курса под воздействием ветра. Дрейф судна создается кажущимся ветром. Направлением ветра называют то направление, откуда он дует (говорят: ветер дует в компас). Если ветер дует в левый борт судна, то говорят судно идет левым галсом (л/г или л/б), по отношению к ветру.

Если ветер дует в правый борт, то судно идет правым галсом (пр/г или пр/б). Направление равнодействующей сил давления ветра (Р) в общем случае не совпадает с направлением вектора скорости кажущегося ветра (W).

Величина угла дрейфа зависит от многих факторов: осадки, размеров и формы надводной и подводной частей корпуса судна, курсового угла и скорости кажущегося ветра, скорости хода судна. Для учета дрейфа при прокладке необходимо знать угол дрейфа. Имеется ряд способов его определения, но все они не являются точными, что приводит иногда к значительному отклонению от намеченного на карте пути.

Разложим эту силу (Р) на две составляющие: продольную (Р₁) и поперечную (Р₂).

(+), а при ветре правого галса знак при угле дрейфа a будет (-).

ПУ_a =- ИК + a. ИК = ПУ_a - a. (1.41)

При учете дрейфа на карте прокладывают только линию путевого угла дрейфа. Так как лаг учитывает влияние ветра на скорость судна (Р₁), то и расстояние можно учитывать, откладывая по линии пути (Sл = РОЛ Кл).

Nи

ИК ПУ_a

a В

А

Р₁

Р₂

Р Рис. 1.25

Расчеты по прямой и обратной задачам удлиняются по сравнению с расчетами без влияния ветра.

Поперечная составляющая Р₂ вызывает дрейф судна. Поэтому при ветре судно перемещается относительно воды не вдоль диаметральной плоскости, а под некоторым углом к ней (a), называемым углом дрейфа. Линия АВ, по которой перемещается судно, называется линией пути при дрейфе, а угол ПУ_a, который она составляет с истинным меридианом, называется путевым углом дрейфа. При ветре левого галса углу дрейфа a присваивается знак (+) плюс, при ветре правого галса – знак (-) минус.

КК = ПУ_a = с карты

+(±)d = из таблицы-(±)a = принят для счисления

МК = ИК =

+(±)d = с карты - (±)d = с карты

ИК = МК =

+(±)a = принят для счисления -(±)d = с карты

ПУ_a = КК =

Nи

ПУ В

DТ Vт

ИК Vл Vт b

А V

Поступательное движение водной массы в морях и океанах называется течением. Элементами течения являются его скорость и направление. Направление течения определяется мнемоническим правилом: «течение идет из компаса». Направление течения показывают в градусах, а иногда в румбах, скорость выражается в узлах.

Под действие упора движителя, судно получает движение относительно воды по направлению диаметральной плоскости (Vл).

Если вода имеет движение относительно Земли, то скорость судна относительно Земли определится геометрической суммой скоростей:

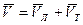
И судно будет перемещаться по направлению вектора 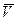, если скорость судна 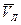и течения 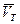постоянны по величине и направлению, суммарная скорость 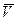также будет неизменна и судно пойдет по прямой АС.

Nи

В

V_m

V_Л

Угол ПУ между северной частью истинного меридиана и направлением движения судна называется путевым углом (путем), а линия пути АС будет линией пути на течении. Угол b между линиями истинного курса (ИК) и путевым углом (ПУ) называется углом сноса от течения.

Скорость V будет истинной скоростью судна (относительно дна).

ПУ = ИК + (±)b ИК = ПУ – (±)b. (1.42)

Знак у b зависит от направления сноса. Если течение направлено в левый борт, то знак у b (+), а если в правый борт, то знак у b (-).

Учет течения сводится к решению треугольников (скоростного и путевого). Вначале графически складывают векторы скоростей судна и течения, а затем решают путевой треугольник АВС.

Различают прямую и обратную задачи графического решения треугольника скоростей. Прямая задача.

В прямой задаче по заданным ИК, Vл, Кт и Vт требуется рассчитать угол b, ПУ и V (Рис.1.27). Для получения линии пути ПУ из точки А проводим линию ИК и на ней от точки А откладываем отрезок, равный вектору скорости судна по лагу (V_Л) в условном масштабе. Обычно берется количество миль в масштабе карты, проходимое судном за час или полчаса. Из конца вектора скорости судна (V_Л) проводим вектор скорости течения (V_Т) в том же масштабе. Соединив точку А с концом вектора скорости течения (Vт), получим

линию пути судна (ПУ). Снимаем с карты направление этого пути для сравнения с истинным

курсом (ИК) и получения угла сноса от течения (b).

b = ПУ – ИК. (1.43)

Для получения счислимой точки за любой временной промежуток плавания по путевому углу, необходимо по линии истинного курса (ИК) отложить пройденное по лагу расстояние (Sл = РОЛ Кл). Полученную на ИК точку сносим по линии направления течения на линию путевого угла (ПУ) (точки В и С). Надписи на карте производятся над или под линией пути (ПУ) и параллельно ей. Порядок записи таков: пишется ГКК рядом в скобках его поправка, а затем величина сноса от течения со своим знаком (ГКК 69° (-2°) b = +6°).

КК =

+(±)d = из таблицы девиации

МК =

+(±)d = с карты

ИК =

+(±)b = из построения

ПУ_b =

Обратная задача

В этой задаче необходимо по заданному ПУ_b, Vл, Кт и Vт рассчитать угол сноса течением (b) и ИК (Рис.1.28).

Задача решается следующим образом:

Пусть на карте проложена линия ПУ (АК). Из точки А прокладываем вектор скорости течения V_T, выраженный количеством миль. Из конца вектора скорости течения V_T раствором циркуля, равным скорости судна V_Л, делаем на линии ПУ судна засечку (точка С). Соединив точку С с концом вектора скорости течения переносим ее параллельно в начальную точку А, проведя линию истинного курса АD.

Нахождение счислимой точки при уже построенном треугольнике скоростей, производится так же, как и в прямой задаче. По расстоянию Sл находим на линии ИК точку В, и затем через точку В проводим линию, параллельную вектору скорости течения Vт. Пересечение этой линии с линией ПУ и будет счислимым местом судна (точка С).

Кроме графического учета течения существует и аналитический, который применяется при автоматизации судовождения.

Nи : D

В

К

Sл С

b

А Vс

Vт

Т Рис.1.28

ПУ_b = направление, снятое с карты

-(±)b = получен расчетным путем (ПУ – ИК)

ИК =

-(±)d = с карты

МК =

-(±)d = из таблицы девиации по МК

КК =

Совместны учет дрейфа течения

При одновременном действии ветра и течения судно будет подвергаться как дрейфу, так и сносу течением. Угол, на который линия пути отклонится от линии истинного курса (ИК), называется суммарным углом сноса (С).

С= ПУ – ИК (1.44)

Знак угла суммарного сноса (С) получается из приведенной формулы: если ПУ >ИК, то знак будет плюс (+), если ПУ < ИК, то знак будет минус (-). Если же известны величины угла дрейфа (a) и угла сноса течением (b), то знак суммарного сноса определится из алгебраического их сложения. С= a + b (1.45)

При наличии ветра и течения решаются также прямая и обратная задачи, как и при наличии только течения. При решении прямой задачи сначала учитывают дрейф и на карту наносят линию пути ПУa. Затем учитывают течение, строя треугольник скоростей, причем скорость судна откладывается по линии путевого угла дрейфа (ПУa), а не по линии ИК.

В обратной задаче при заданном ПУ решают треугольник скоростей, при этом из построения получают не направление ИК, а направление ПУa. Затем снимают направление пути дрейфа (ПУa) и находят истинный курс: ИК = ПУa - a, а также

b = ПУ - ПУa и С= a + b.

На карте под (или над) линией путевого угла делается запись о компасном курсе, его поправке и о суммарном угле сноса (ГКК (-2) С= -12)

В общем виде решение задачи выглядит таким образом:

Прямая задача Обратная задача

КК = ПУ =

+(±)d = из таблицы девиации - (±)b = из построения

МК = ПУa =

+(±)d = с карты-(±)a = принятый

ИК = ИК =

+(±)a = принятый для счисления - (±) d = с карты

ПУa = МК =

+(±)b =-(±) d = из таблицы дв.

ПУ = КК =

Пример 1. В широте j = 53°00¢ N судно следует ИК = 75,0° со скоростью 12 узлов. Учитывается течение 335° – 1,1 узла. Определить угол сноса судна течением b.

Решение: От исходной точки, от которой проложен ИК = 75,0°. Откладываем расстояние, пройденное судном за один час (скорость судна) S_Л.

От полученной точки на ИК откладываем по направлению течения снос судна течением за один час (скорость течения) S_Т = 1,1 мили.

Соединяем исходную точку с полученной на векторе течения и с помощью параллельной линейки и транспортира снимаем отсчет ПУ = 69,0°.

Рассчитываем угол сноса течением b.

ПУ = 69,0°

- ИК = 75,0°

b = - 6,0°

Пример 2. В широте j = 53°00¢ N судно следует, имея скорость по лагу 12 узлов. На карте от исходной точки проложен ПУ = 52,8°. На судне учитывается течение 143° – 1,0 узел. Определить ИК и b.

Решение: Из исходной точки проводим линию направления течения и на ней откладываем отрезок, равный скорости течение V_T=1.0 узл.

Из полученной точки радиусом, равным скорости судна 12 узлов, на линии ПУ делаем засечку и соединяем обе точки прямой.

С помощью параллельной линейки транспортира снимаем значение ИК = 48,8°

Рассчитываем угол сноса течением b.

ПУ = 52,8°

- ИК = 48,0°

b = + 4,8°

Пример 3. Дано: ПУ = 356,6°, b = - 6,2°, a = + 4,0°, D_ГКК = -1,2°. Определить ГКК.

Решение: ПУ = 356,6

- b = - 6,2

ПУ_a = 002,8

- a = +4,0

ИК = 358,8

- D_ГКК = -1,2

ГКК = 360,0

Пример 4. Рассчитать радиальную СКП счисления без учета влияния ветра и течения, если судно прошло 100 миль.

Решение: Из НШСР -86 (таблица № 3) выбираем m_K = 0,7°, m_DЛ% = 0,5%, тогда

b = 0,0174 * 0,7 * 100 = 1,218

a = 0,01 * 0,5 * 100 = 0,5

M = Öb² + a² = Ö1,48 + 0,25 = 1, 3 мили.

Контрольные вопросы

1. Какой знак (+) или (-) присваивается углу дрейфа правого борта?

2. Направление течения считается в «компас или из компаса»?

3. Как рассчитать общий снос от ветра и течения при известных ПУ, ПУa, ИК?

4. Какая приближенная зависимость СКП графического счисления от пройденного расстояния?

5. С чего начинают решение обратной навигационной задачи при учете течения?