Меридиональные части

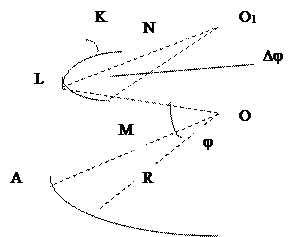
Для упрощения решения задачи примем форму Земли в виде шара. Рассмотрим элементарный треугольник на поверхности шара D LMN и его проекцию на плоскость D lmn (Рис.1.10 и 1.11).

При проектировании треугольника с поверхности шара на плоскость, меридианы изобразятся параллельными прямыми, перпендикулярными линии экватора, а параллели прямыми, параллельными экватору. По малости треугольника D LMN можно рассматривать его как плоский и прямоугольный.

Тогда катет È MN = а Dj,

а катет È LM = r Dl = аDl Cosj.

В треугольнике D LMN отношение катетов будет:

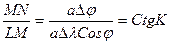
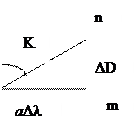
В элементарном треугольникеlmn катеты будут по меридиану dx, а по параллели - dy, но dy = adl. Переходя к конечным приращениям, имеем dx =DD, dy=aDl.

	PN

		l

	B		a		b

Тогда в треугольнике D lmn на плоскости, отношение катетов запишется:

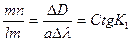
Исходя из подобия треугольников и равенства углов, можно записать:

,

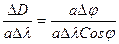откуда 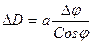, переходя из конечных приращений к дифференциалам, получим:

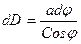. (1.17)

Проинтегрировав выражение (1.17) в пределах от 0 до j, получим:

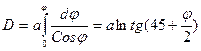(1.18)

Величина D называется меридиональной частью и представляет собой расстояние по меридиану от экватора до заданной параллели в минутах дуги экватора.

Выражая меридиональную часть через длину дуги экватора, примем:

а = 3437,747 экв. миль.

Далее для перехода от натуральных логарифмов к десятичным, введем модуль логарифмов: mod = 0,434294.

Тогда: D = .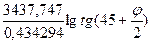

D = 7915,705 lgtg(45 + 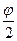) (1.19)

С учетом сжатия Земли выражение перепишется в следующем виде:

D¢ = 7915,70447 lg tg (45 + 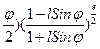(1.20)

По этой формуле составлены таблицы «Меридиональные части» в МТ любого года издания.

Пример 1:

Во сколько раз меркаторская миля в широте j₁ = 71°30 больше меркаторской мили в широте j₂ = 26°30¢?

Решение. Из мореходных таблиц выбираем значения меридиональных частей для приведенных в задаче широт

j₁ = 71°30 МЧ = 6217,2 j = 71°31 МЧ = 6220,4

j₂ = 26°30¢ МЧ = 1639,7 j = 26°31 МЧ = 1640,8

Для j₁ при РШ = 1¢ РМЧ₁ = 3,2

Для j₂ при РШ = 1¢ РМЧ₂ = 1,1.

Вычисляем отношение полученных РМЧ и тем самым находим ответ на поставленный вопрос задачи: 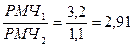раза.

Пример 2: Рассчитать длину одной минуты меридиана в широте Одессы j = 46°35¢N.

Решение. Для расчета применим формулу: S = 1852,25 – 9,31 Cos2j. Подставив значение широты 46°35¢, получим длину одной минуты меридиана в метрах:

S = 1852,2 – 9,31 Cos 93°10¢ = 1852,2 – 9,31 * 0,0552 = 1851,7 м.

Контрольные вопросы

1. Единица измерения меридианного радиуса кривизны сечения эллипсоида.
2. Как изменяется длина 1¢ меридиана в зависимости от широты?
3. Что такое меридиональная часть?
4. Перечислите основные свойства локсодромии.
5. Чему равна длина 1 морской мили в метрах?