Географическая дальность видимости горизонта
Видимость играет огромное влияние на безопасность мореплавания. Безопасная скорость судна (Правило № 6 МППСС-72) назначается с учетом текущей видимости и других обстоятельств плавания. Совершенно необходима техника, которая бы автоматически определяла состояние видимости и фиксировала ее.
Высота глаза наблюдателя над уровнем моря в точке А1 равна е. Решаем эту задачу, чтобы выяснить, как далеко наблюдатель видит линию горизонта. Рассмотрим эту проблему на сфере радиусом R. Такое представление поверхности Земли будет достаточным и упростит решение задачи (Рис.1.12)
 |
|

|



 е r d
е r d

 A а
A а
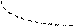 K
K
r
 |
|
|
|
 R
R





 E ρ С Q
E ρ С Q
|
 |
| |
|
Луч зрения из точки А1, касательный к поверхности воды по всем направлениям образует малый круг (К1 К), который называется линией теоретически видимого горизонта.
Вследствие различной плотности атмосферы по высоте, луч света распространяется не прямолинейно, а по некоторой кривой ÈА1 В, которая определяется окружностью радиуса ρ.
Явление искривления луча в атмосфере Земли называется земной рефракцией и обычно увеличивает теоретическую дальность видимости горизонта.
Таким образом, наблюдатель видит линию горизонта не по К1 К, а по линии В1 В, которая является малым кругом, касающимся небосвода. Это видимый горизонт наблюдателя.
Коэффициент земной рефракции (хи - χ) равен: χ = 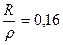 .
. 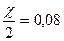
Угол рефракции r определяется углом между хордой А1 В и касательной к окружности радиуса ρ. Сферический радиус по поверхности Земли А1 В называется географической или геометрической дальностью видимого горизонта Dе.
При этом принимается прозрачность атмосферы идеальной и равной (t = 1) единице.
Проведем через точку А1 плоскость истинного горизонта Н. Тогда угол d между этой плоскостью и касательной А1а будет называться наклонением горизонта.
Теперь рассмотрим зависимость между географической дальностью видимости горизонта De, высотой глаза наблюдателя e и коэффициентом рефракции c. Напишем значения дуг (сферы распространения зрительного луча) через их параметры:
ÈАВ = RC
Радиус ρ перпендикулярен касательным А1а и Вb, тогда
ÐО1 = 180 – 2(90-r) = 2r, ÈA1B = 2ρr
 По малости е по сравнению с ÈАВ и ÈА1В запишем: ÈАВ = ÈA1B или
По малости е по сравнению с ÈАВ и ÈА1В запишем: ÈАВ = ÈA1B или
RC = 2ρr, откуда:
r = 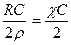 ,
, 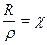 ,
, 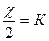 , r = KC
, r = KC
Теперь рассмотрим D ОАВ:
ÐВ = 90-r, ÐA1 = 180 – C –(90-r) = 90 – (C-r)
По теореме синусов имеем:
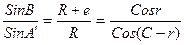 (1.21)
(1.21)
Преобразуем полученное выражение как:
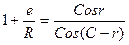 ,
, 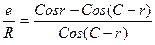
Исходя из того, что
Cos r – Cos(C-r) = - 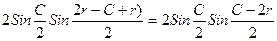
Будем иметь
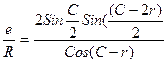 .
.
Величины углов С и r малы и без потери точности, заменим тригонометрические функции их первыми членами разложения в ряд:
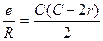 ; r = KC
; r = KC
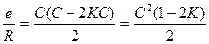
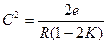 , так как С =
, так как С = 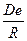 , то
, то 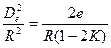
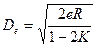 (1.22)
(1.22)
При R=3437,76 мили c=2К =0,16 высоту глаза наблюдателя евыразим как единицу длины в милях 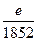 , тогда:
, тогда: 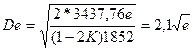 миль,
миль,
De = 2,1Öe (1.23)
В МТ-75 приведена таблица дальности видимости горизонта, рассчитанной по выше приведенной формуле.
Дата добавления: 2015-08-26; просмотров: 861;
