Ортодромия локсодромия
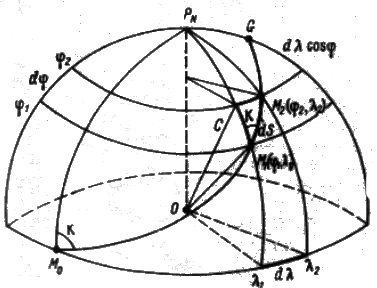
Используя навигационные морские карты, судоводители прокладывают на них путь в виде прямой линии. Из условия построения карты, такой прямой путь на карте не будет кратчайшим на местности. Путь (прямая), проложенный на карте в Меркаторской проекции называется локсодромией (кривой бег). Кратчайший же путь между двумя точками на земной поверхности эллипсоида является сложной кривой, называемой геодезической линией. На поверхности сферы (шара) кратчайшее расстояние между двумя точками измеряется по дуге большого круга, т.е. круга, образованного пересечением плоскости, проходящей через центр сферы и заданные точки, со сферической поверхностью. Такая дуга в навигации называется ортодромией (Рис.1.6). Уравнение ортодромии, проходящей через заданные точки, имеет вид:
CtgA1 = tgj2 Cosj1CosecDl - Sinj1 CtgDl (11), где:
А1 – направление ортодромии в точке В1,
Dl - разность долгот точек В2 и В1.
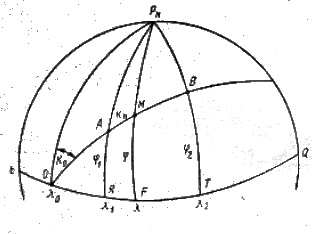 При анализе уравнения ортодромии можно сделать следующие выводы:
При анализе уравнения ортодромии можно сделать следующие выводы:
1. при расположении точек В1 и В2 на одном меридиане ортодромия совпадает с меридианом этих точек.
2. ортодромия пересекает меридианы под разными углами (А0 , А1 , А2),
3. при расположении точек по экватору ортодромия совпадает с экватором.
|
Разность углов, под которыми ортодромия пересекает меридианы двух точек, называется сближением (схождением) меридианов. γ = А2 – А1.
Угол схождения меридианов рассчитывается по приближенной формуле:
γ = 2arc tg [tg( 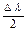 ) Sin jср] (1.14)
) Sin jср] (1.14)
Основные свойства локсодромии:
- Если курс равен 180 или 360, то локсодромия совпадает с меридианом и ортодромией (см 1.6) К=0. tgK = 0. l2 - l1 = 0. . l2 = l1 )
- Если курс равен 90 или 270, то локсодромия совпадает с параллелью или экватором, т.е. образует малый или большой круг на поверхности Земли.
- При любых других курсах локсодромия спиралеобразно стремится к полюсу, никогда его не достигая.
|
|
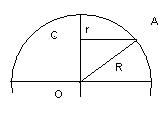
ному на косинус широты этой параллели.
Возьмем на локсодромии две точки М1(j1, l1) и М2(j2, l2) (Рис. 1.8a), находящиеся на малом расстоянии одна от другой (dS). Из элементарного треугольника М1 М2 С (Рис.18.b) имеем:
tgK= 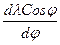 ,откуда dl = tgK
,откуда dl = tgK 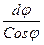 , проинтегрировав это последнее выражение, получим:
, проинтегрировав это последнее выражение, получим:
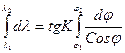 , после решения интегралов,
, после решения интегралов,
|
|
|
|
|
|
|

|


получим уравнение локсодромии:
l2 - l1 = tg K [ln tg(p/4+j2/2) – ln tg (p/4 + j1/2)] (1.15)
Возвращаясь к форме Земли как сфероиду, локсодромия примет вид:
l2 - l1 = tg K 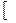 ln tg (
ln tg ( 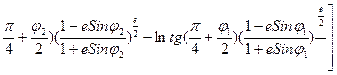
локсодромия на навигационной карте:
y – y0 = (x – x0) tgK, (l - l0)¢ = (D – D0)¢ tg K,
РД = РМЧ tg K (1.16)
 |
 D
D
 Рис.1.9
Рис.1.9
|
l0 l
Дата добавления: 2015-08-26; просмотров: 1235;
