Главные радиусы кривизны сечения меридианного эллипса

Зная значения координат точки на меридианном эллипсе в прямоугольной системе, определим значения главных радиусов кривизны меридианного сечения М и нормального к нему сечения N. Кривизна любой кривой определяется соотношением:

М = ç 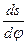ç (1.7)

Из треугольника АВС, приведенного на Рис.1.4, имеем:

ds = - 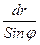, знак (-) говорит о том, что с увеличением широты (j) радиус (r) уменьшается.

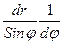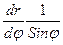Тогда: М = ç ç = , но dr = dx, тогда

М = 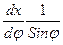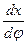получим, если продифференцируем значение х в прямоугольных координатах (1.5).

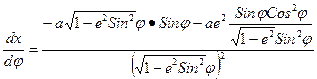, после преобразования получим:

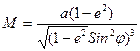(1.8)

Здесь: j - географическая широта

а – большая полуось Эллипсоида Красовского, а = 6378245м

е² – квадрат первого эксцентриситета е² = 0,0066934

Нормальный радиус эллипса (N) зависит от координаты х как

N = 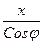, после подстановки выражения х получим:

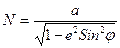(1.9)

и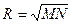

Где М – меридианный радиус кривизны,

N- нормальный радиус кривизны,

R – средний радиус кривизны.