Класифікація математичних моделей
В залежності від специфіки зв’язку між характеристиками стану та вхідними даними розрізняють детермінованітастохастичні математичні моделі. В детермінованих моделях у кожний фіксований момент часу характеристики стану системи (об’єкта моделювання чи проектування) однозначно визначаються через вхідні дані. Детерміновані моделі будують на основі фундаментальних теоретичних законів, таких як закони збереження енергії, маси, закони термодинаміки, кінетики тощо. Усі величини, які входять до складу детермінованих моделей задають у вигляді конкретних чисел, векторів та функцій. Якщо хоча б один параметр системи (об’єкта моделювання чи проектування) приймає випадкові значення, то таку побудовану математичну модель будемо називати стохастичною. У цьому випадку під однозначністю визначення характеристик стану системи розуміють однозначність визначення ймовірністного розподілу цих характеристик за заданими розподілами ймовірностей вхідних даних. В принципі будь-якій реальній системі притаманні в тій чи іншій мірі випадкові флуктуації. Тому, якщо під час моделювання такої системи впливом цих випадкових факторів не можна знехтувати, то доводиться будувати і досліджувати стохастичну модель. У протилежному випадку достатньо обмежитися детермінованою моделлю. Виокремлення детермінованих моделей в окремий клас можна пояснити широким використанням та різноманітністю математичних методів їх дослідження.
В більш загальному випадку можемо стверджувати, що в детермінованих математичних моделях інженер чи науковець оперує лише математичними очікуваннями параметрів об’єкта моделювання, а в стохастичних – випадковими розподілами цих параметрів (чи хоча б випадковим розподілом одного з цих параметрів ММ).
Розрізняють також лінійні та нелінійні, розподілені та зосереджені за просторовими координатами, неперервні та дискретні, стаціонарні та нестаціонарні математичні моделі.
Математична модель називаєтьсялінійною, якщо для оператора моделі виконується принцип суперпозиції. У протилежному випадку модель називається нелінійною. Нелінійні моделі, в свою чергу, можна поділити на алгебричні та трансцендентні. У рівняннях нелінійної алгебраїчної моделі над змінними проводяться лише звичайні арифметичні операції та операції піднесення до степеня з раціональним показником, а в рівняння нелінійної трансцендентної моделі можуть входити інші функції над змінними (тригонометричні, логарифмічні і т.д.). Більшість реальних систем є нелінійними, хоча на практиці, найчастіше використовуються лінійні моделі, які з задовільною точністю описують поведінку таких систем і є більш доступними для дослідження.
В нестаціонарних моделях вихідні параметри (рішення задачі) змінюються з часом, в іншому випадку – вихідні параметрі не залежать від змінної часу. Неперевні моделі дають змогу визначити зміну вихідних параметрів в будь-який момент часу (для прикладу, модель, яка дає змогу визначити вихідні параметри аналогового електричний сигналу). Дискретні моделі оперують дискретною інформацією, тобто даними, отриманими в певні відлікі часу (наприклад, моделі, що оперують з цифровою формою представлення електричного сигналу).
Важливий клас математичних моделей складають так звані подібні моделі, які забезпечують перехід до оригіналу на основі теорії подібності.
Основні ознаки класифікації та типи математичних моделей, які використовуються в системах автоматизованого проектування (САПР) наведено в таблиці 2.1.
Таблиця 2.1
| Ознака класифікації | Математичні моделі |
| Характер відображених властивостей об’єкта | Структурні, функціональні |
| Приналежність до ієрархічного рівня | Мікрорівня, макрорівня, метарівня |
| Степінь деталізації опису в середині кожного рівня | Повні, макромоделі |
| Спосіб представлення властивостей об’єкта | Аналітичні, алгоритмічні, схемні, імітаційні |
| Спосіб отримання моделі | Теоретичні, емпіричні |
За характером відображених властивостей об'єкта ММ поділяються на структурні та функціональні.
Структурні ММпризначені для відображення структурних властивостей об'єкта.Структурні математичні моделі поділяються натопологічні й геометричні.
Функціональниминазивають такі математичні моделі, які дають змогу визначити вихідні параметри об’єкта моделювання на основі вхідних та зовнішніх.
Топологічні ММ відображають склад і взаємозв’язки між елементами об'єкта. Найчастіше їх застосовують для опису об'єктів, які складаються з великого числа елементів, при розв’язанні задач прив'язки конструктивних елементів до певних просторових позицій (наприклад, задачі компонування обладнання, розміщення деталей, трасування з'єднань) чи до відносних моментів часу (наприклад, при розробці розкладів руху громадського транспорту, технологічних процесів). Топологічні моделі можуть мати форму графів, таблиць (матриць), списків тощо.
Геометричні MM відображають геометричні властивості об'єктів, у них додатково до інформації про взаємне розташування елементів містяться дані про форму деталей. Геометричні ММ можуть виражатися сукупністю рівнянь ліній і поверхонь; алгебричних співвідношень, які описують області, що складають тіло об'єкта; графами і списками, що відображають конструкцію з типових конструктивних елементів, тощо. Геометричні ММ застосовують при розв’язанні задач конструювання в машинобудуванні, приладобудуванні, радіоелектроніці, для оформлення конструкторської документації, при задані вихідних даних на розробку технологічних процесів виготовлення деталей.
Використання принципів блочно-ієрархічного підходу до проектування приводить до появи ієрархії математичних моделей проектованих об'єктів. Кількість ієрархічних рівнів, при моделюванні, визначається складністю проектованих об'єктів, технологіями, які використовують в процесі проектування і можливістю засобів проектування. Однак для більшості прикладних областей можна віднести наявні ієрархічні рівні до одного з трьох узагальнених рівнів, названих надалі мікро-, макро- і метарівнями.
В залежності від місця в ієрархії математичні моделі поділяються на ММ, які відносяться до мікро-, макро- і метарівнів.
Особливістю ММ на мікрорівні є відображення фізичних процесів, що протікають в об'єкті та неперервні в просторі і часі. Типові ММ на мікрорівні включають диференціальні рівняння в часткових похідних (ДРЧП). В них незалежними змінними є просторові координати та час. З допомогою цих рівнянь розраховують поля механічних напруг і деформацій, електричних потенціалів, тисків, температур тощо. Можливості застосування ММ у виді ДРЧП обмежені окремими деталями, спроби аналізувати з їхньою допомогою процеси в багатокомпонентних середовищах, складальних одиницях, електронних схемах не можуть бути успішними через надмірний ріст витрат машинного часу і пам'яті персонального комп’ютера.
На макрорівні використовують дещо грубішу дискретизацію простору по функціональному признаку, що приводить до представлення ММ на цьому рівні у виді систем звичайних диференціальних рівнянь (ЗДР). В цих рівняннях незалежною змінною є час 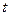 , а вектор залежних змінних складає фазові змінні, які характеризують стан елементів дискретизованного простору. Такими змінними є сили і швидкості в механічних системах, напруги і сили струму в електричних системах, тиски та витрати в гідравлічних і пневматичних системах тощо. Системи ЗДР є універсальними моделями на макрорівні, придатними для аналізу як динамічних, так і статичних режимів роботи об'єктів моделювання. Моделі для стаціонарних режимів можна також представити у виді систем алгебричних рівнянь. Порядок системи рівнянь залежить від числа виділених елементів об'єкта. Якщо порядок системи наближається до 100, то оперувати такою моделлю стає важко і тому необхідно переходити до представлення моделі на метарівні.
, а вектор залежних змінних складає фазові змінні, які характеризують стан елементів дискретизованного простору. Такими змінними є сили і швидкості в механічних системах, напруги і сили струму в електричних системах, тиски та витрати в гідравлічних і пневматичних системах тощо. Системи ЗДР є універсальними моделями на макрорівні, придатними для аналізу як динамічних, так і статичних режимів роботи об'єктів моделювання. Моделі для стаціонарних режимів можна також представити у виді систем алгебричних рівнянь. Порядок системи рівнянь залежить від числа виділених елементів об'єкта. Якщо порядок системи наближається до 100, то оперувати такою моделлю стає важко і тому необхідно переходити до представлення моделі на метарівні.
Метарівень характеризується великою розмаїтістю типів ММ. Для багатьох об'єктів ММ на метарівні, як і раніше, представляють системами ЗДР. Однак, тому що в моделях не описуються внутрішні для елементів фазові змінні, а фігурують лише фазові змінні, які відносяться до взаємних зв'язків між елементами. Укрупнення елементів на метарівні означає одержання ММ прийнятної розмірності для значно більш складних об'єктів, ніж на макрорівні.
В ряді предметних областей вдається використовувати специфічні особливості функціонування об'єктів для спрощення ММ. Прикладом є електронні пристрої цифрової автоматики, в яких можливо застосовувати дискретне представлення таких фазових змінних, як напруги та струми. В результаті ММ стає системою логічних рівнянь, що описують процеси перетворення сигналів. Такі логічні моделі істотно більш економічні, ніж моделі електричні, що описують зміни напруг і сил струмів як функцій часу. Важливий клас ММ на метарівні складають моделі на основі систем масового обслуговування, що використовуються для опису процесів функціонування інформаційних і обчислювальних систем, виробничих ділянок, ліній і цехів.
За ступенем деталізації опису об’єктів моделювання в межах кожного ієрархічного рівня виділяють повні ММ і макромоделі.
Повна MM – модель, в якій фігурують фазові змінні, що характеризують стани всіх наявних між елементних зв'язків (тобто стану всіх елементів проектованого об'єкта).
Макромодель – ММ, у якій відображаються стани значно меншого числа міжелементних зв'язків, що відповідає опису об'єкта при укрупненому виділенні елементів.
За формою представлення математичні моделі поділяють на інваріантні, аналітичні й алгоритмічні та схемні [3].
Інваріантна форма запису відношень моделі передбачає використання традиційної мови математики не залежно від методу розв’язання задачі.
Аналітичні ММ являють собою явні вирази вихідних параметрів як функцій вхідних, внутрішніх та зовнішніх параметрів об'єкта моделювання. Такі ММ характеризуються високою економічністю, однак одержання такої форми вдається лише в окремих часткових випадках, як правило, при прийнятті певних спрощень і обмежень, що знижує точність і звужує область адекватності моделі. Приклад таких моделей зображено у формі виразів (2.1 та 2.2).
Схемна форма представлення ММ передбачає використанням деякої графічної мови, а саме: графів, еквівалентних схем, діаграм тощо. Прикладами таких моделей можуть бути еквівалентна схема транзистора чи електромеханічного актюатора, модель у формі мережі Петрі електромеханічної системи, граф фрагмента електричної схеми та ін. Відповідні моделі, як правило, використовують на системному та функціонально-логічному рівнях автоматизованого проектування і дещо рідше на схемотехнічному.
Алгоритмічні ММ виражають зв'язки вихідних параметрів з вхідними, внутрішніми та зовнішніми параметрами у формі алгоритму. Типовою алгоритмічною математичною моделлю є система рівнянь доповнена алгоритмом чисельного методу розв’язання й алгоритмом обчислення вектора вихідних параметрів як функціоналів розв’язання системи рівнянь. Прикладами таких моделей можуть бути вирази (2.4) і (2.5), якщо додати початкові та краєві умови з алгоритмами розв’язання сформульованих задач. В більшості випадків, алгоритмічні моделі використовують на схемотехнічному та компонентному рівнях автоматизованого проектування, хоча можливе їх використання і на вищих рівнях абстракції.
Особливим підвидом алгоритмічних математичних моделейє імітаційні. Імітаційна – алгоритмічна модель, яка відображає поведінку досліджуваного об'єкта в часі при задані зовнішніх впливів на об'єкт. Прикладами імітаційних ММ можуть бути моделі динамічних об'єктів у виді систем ЗДР і моделі на основі систем масового обслуговування, задані в алгоритмічній формі.
При одержанні ММ використовують неформальні і формальні методи. Неформальні методи застосовують на різних ієрархічних рівнях для одержання ММ елементів. Ці методи включають вивчення закономірностей процесів і явищ, зв'язаних з об’єктом моделювання, виділення істотних факторів, прийняття різного роду допущень і їхнє обґрунтування, математичну інтерпретацію наявних процесів і т.п. Для виконання цих операцій, в загальному випадку, відсутні формальні методи, в той же час, від результату цих операцій істотно залежать показники ефективності MM - ступінь універсальності, точність та економічність. Тому, побудова ММ елементів, як правило, здійснюється кваліфікованими фахівцями, які одержали підготовку як у відповідній предметній області, так і в питаннях математичного моделювання на електронно-обчислювальній машині.
Застосування неформальних методів можливо для синтезу теоретичних і емпіричних ММ. Теоретичні ММ створюються в результаті дослідження процесів і їхніх закономірностей, властивих розглянутому класу об'єктів і явищ. Емпіричні MM - в результаті вивчення зовнішніх проявів властивостей об'єкта за допомогою вимірів фазових змінних на зовнішніх входах і виходах та обробки результатів вимірів.
Рішення задач моделювання елементів полегшується завдяки тому, що для побудови більшості технічних об'єктів використовуються типові елементи (кількість типів порівняно невелика). Тому розробка ММ елементів виконується порівняно рідко. Одноразово побудовані ММ елементів надалі багаторазово застосовують при розробці різноманітних систем з цих елементів.
Формальні методи застосовують для одержання ММ систем при відомих математичних моделях елементів.
Таким чином, у програмах автоматизованого синтезу та аналізу, які використовують в САПР, одержання ММ проектованого об'єкта забезпечується реалізацією ММ елементів і методів формування ММ систем.
Дата добавления: 2015-08-26; просмотров: 2696;
