Види опису математичних моделей
В загальному випадку під математичною моделлю (ММ) розуміють будь-який математичний опис, що відображає з потрібною точністю структуру та/або процес функціонування деякої реальної системи в реальних умовах. Визначення математичної моделі, що враховує специфіку та особливості автоматизованого проектування є наступне: математична модель це набір математичних знаків для встановлення зв’язку між вихідними та вхідними і внутрішніми параметрами об’єкта проектування в заданих умовах. Отже, математичний опис полягає у встановленні зв’язків між параметрами процесу та виявлені його граничних і початкових умов, а також у формалізації цього процесу у вигляді системи математичних співвідношень.
У найпростішому випадку математичний опис (математична модель) об’єкта проектування має вигляд явної функції, що виражає змінну величину (вихідні параметри) через інші змінні, які називаються аргументами (вхідні, внутрішні та параметри зовнішнього середовища), і в загальному випадку може бути записана наступним чином:
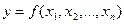 , (2.1)
, (2.1)
де 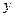 – вихідний параметр моделі,
– вихідний параметр моделі, 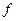 – функція перетворення,
– функція перетворення, 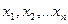 – множина вхідних, внутрішніх та параметрів зовнішнього середовища.
– множина вхідних, внутрішніх та параметрів зовнішнього середовища.
Прикладом такої математичної моделі може бути вираз для визначення величини електростатичної сили 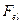 , що виникає між пластинами плоского конденсатора:
, що виникає між пластинами плоского конденсатора:
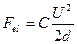 ,
, 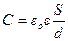 , (2.2)
, (2.2)
де 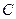 – електрична ємність;
– електрична ємність; 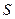 – площа пластин;
– площа пластин;  – прикладена напруга;
– прикладена напруга; 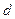 – відстань між пластинами конденсатора;
– відстань між пластинами конденсатора; 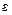 ,
, 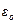 – діелектрична проникність середовища між пластинами конденсатора та діелектрична проникність у вакуумі.
– діелектрична проникність середовища між пластинами конденсатора та діелектрична проникність у вакуумі.
В більш складному випадку ММ має вигляд рівняння такого виду:
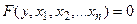 , (2.3)
, (2.3)
яке виражає залежність (2.1) в неявній формі. Наприклад це моделі, що описують залежності між її параметрами з допомогою трансцендентних рівнянь, систем лінійних алгебричних рівнянь (СЛАР) тощо.
У складнішому випадку співвідношення математичної моделі можуть бути записані у формі звичайних диференціальних рівнянь
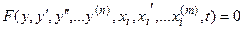 , (2.4)
, (2.4)
які зв’язують незалежну змінну 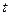 , відомі функції
, відомі функції 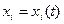 , невідому функцію
, невідому функцію  та похідні функцій
та похідні функцій 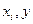 . Прикладом такої ММ може бути диференціальне рівняння другого порядку, що описує зміщення пластини електричного конденсатора під дією зовнішньої сили з врахуванням електростатичної сили (2.2) між його пластинами
. Прикладом такої ММ може бути диференціальне рівняння другого порядку, що описує зміщення пластини електричного конденсатора під дією зовнішньої сили з врахуванням електростатичної сили (2.2) між його пластинами
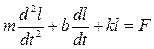 ,
, 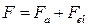 ,
,
де 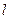 – зміщення;
– зміщення; 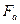 – механічна сила;
– механічна сила; 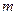 – маса пластини;
– маса пластини; 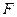 – сумарна прикладена сила;
– сумарна прикладена сила; 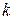 – коефіцієнт пружності пружини;
– коефіцієнт пружності пружини; 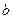 – коефіцієнт демпферування.
– коефіцієнт демпферування.
В загальному випадку до цієї групи входять моделі, що описують процеси з використанням систем звичайних диференціальних рівнянь, диференціальних рівнянь 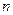 -го порядку тощо.
-го порядку тощо.
І, нарешті, математична модель може включати диференціальні рівняння в частинних похідних
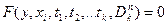 , (2.5)
, (2.5)
в яких, на відміну від звичайних диференційних рівнянь, шукана функція 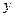 залежить від декількох незалежних змінних, наприклад, температура може залежати від просторових координат та часу. Тут через
залежить від декількох незалежних змінних, наприклад, температура може залежати від просторових координат та часу. Тут через 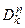 позначено часткову похідну
позначено часткову похідну 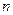 -ого порядку від змінної
-ого порядку від змінної 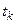 .
.
Прикладом таких моделей є ММ, що описує переміщення тонкої пластини, при цьому припускається, що розподіл сили по пластині є рівномірний, а її краї - жорстко защемлені:
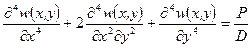 ,
, 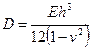 ,
,
де 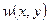 – прогини пластини (вертикальні переміщення пластини);
– прогини пластини (вертикальні переміщення пластини); 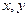 – осі, які формують координатну площину
– осі, які формують координатну площину 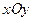 , що рівновіддалена від основ пластини;
, що рівновіддалена від основ пластини; 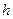 – товщина пластини;
– товщина пластини; 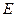 – модуль пружності матеріалу пластини;
– модуль пружності матеріалу пластини; 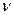 – коефіцієнт Пуассона матеріалу пружного елемента;
– коефіцієнт Пуассона матеріалу пружного елемента; 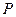 – інтенсивність розподіленого на поверхні пластини навантаження.
– інтенсивність розподіленого на поверхні пластини навантаження.
Необхідно зауважити, що коректне формулювання вищенаведеної моделі потребує визначення ще крайових умов.
Співвідношення (2.1, 2.2 – 2.5) можна узагальнити використовуючи поняття оператора. Розглянемо деяку систему стан якої, в довільний момент часу 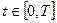 , описується певним набором
, описується певним набором 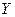 - величин, які називаються характеристиками стану. Характеристики стану залежать як від власних параметрів системи, так і різних зовнішніх впливів з боку оточуючого середовища. Опис цієї залежності – це і є суть математичної моделі цієї системи. В загальному випадку, характеристики стану, власні параметри та зовнішні фактори є функціями одного і того ж або різних аргументів. Правила перетворення однієї функції в іншу називають оператором. Тоді математична модель, в найбільш загальному випадку, має наступний операторний вигляд:
- величин, які називаються характеристиками стану. Характеристики стану залежать як від власних параметрів системи, так і різних зовнішніх впливів з боку оточуючого середовища. Опис цієї залежності – це і є суть математичної моделі цієї системи. В загальному випадку, характеристики стану, власні параметри та зовнішні фактори є функціями одного і того ж або різних аргументів. Правила перетворення однієї функції в іншу називають оператором. Тоді математична модель, в найбільш загальному випадку, має наступний операторний вигляд:
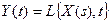 , (2.6)
, (2.6)
де через 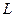 позначено оператор, а під
позначено оператор, а під 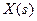 розуміється набір величин, які тим чи іншим способом впливають на характеристики стану. Частковим випадком такого оператора є функціонал, який задає правила перетворення функції в скалярну величину.
розуміється набір величин, які тим чи іншим способом впливають на характеристики стану. Частковим випадком такого оператора є функціонал, який задає правила перетворення функції в скалярну величину.
Наведене вище тлумачення оператора як правила перетворення функцій можна узагальнити наступним чином. Нехай задано дві множини функцій  та
та 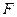 і нехай функція
і нехай функція 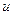 є елементом множини
є елементом множини  , функція
, функція 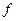 - множини
- множини 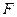 , тобто
, тобто 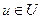 ,
, 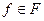 . Тоді в операторному рівнянні
. Тоді в операторному рівнянні
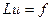 , (2.7)
, (2.7)
оператор 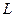 задає відповідність між елементами множин
задає відповідність між елементами множин  і
і 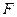 , а розв’язати операторне рівняння (2.7) означає знайти
, а розв’язати операторне рівняння (2.7) означає знайти 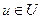 при заданих
при заданих 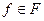 та вигляд оператора
та вигляд оператора 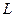 .
.
Для побудови математичних моделей можуть використовуватися як універсальні фундаментальні закони природи (закони збереження маси, енергії, другий закон Ньютона), так і феноменологічні закони (закон Гука, закон Фур’є), тобто достатньо добре емпірично обґрунтовані закони з обмеженою областю дії (яка також встановлена емпірично). Математичний опис завжди є відображенням фізичної сутності деякого реального об’єкту з його характерними особливостями та обмеженнями. Математична модель концентрує у вигляді математичних співвідношень сукупність наших знань, уявлень та гіпотез про відповідний об’єкт дослідження. Вона (математична модель) завжди описує поведінку реальної системи лише наближено, оскільки наші знання не є абсолютними, а гіпотези та припущення не враховують усі фактори. Тому, математичні моделі відносяться до класугомоморфних моделей (макромодель), під якими розуміють моделі, що відображають лише основні властивості об’єкту дослідження, причому між гомоморфною моделлю та оригіналом відсутнє повне, поелементне відображення. На відміну від гомоморфних, в ізоморфнихмоделях спостерігається повна поелементна відповідність між моделлю та оригіналом (повна модель).
Дата добавления: 2015-08-26; просмотров: 1085;
