ТЕОРЕМА КОТЕЛЬНИКОВА. ВЫБОР ЧАСТОТЫ ДИСКРЕТИЗАЦИИ
Теорема Котельникова – любой непрерывный сигнал, ограниченный по спектру верхней частотой Fв полностью определяется последовательностью своих дискретных отсчетов взятых через промежуток времени ∆t = Тд≤1/2Fв.
Тд — период дискретизации,
Fд — частота дискретизации,
Fв — верхняя частота.
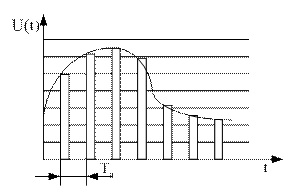

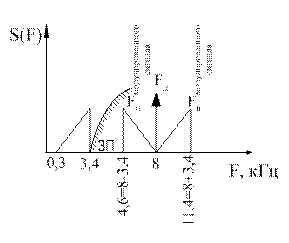
| Т.о., если требуется передать непрерывный сигнал U(t) с ограниченным спектром, то не обязательно передавать весь сигнал, а достаточно передать лишь его мгновенные значения, отсчитанные через интервалы времени Тд. В соответствии с этим частота следования дискретных отсчетов сигнала, т.е. частота дискретизации Fд ≥2Fв. Если Fд =2Fв. Нижняя боковая частота промодулированного сигнала, определяемого из условия Fд -Fв= =2Fв- Fв= Fв, совпадает с верхней частотой спектра модулирующего сигнала, таким образом, для восстановления непрерывного сигнала по его дискретным отсчетам необходимо использовать идеальный ФНЧ с частотой среза Fср = Fв. В реальных системах Fд выбирают из условий Fд>2Fв. Fд=(2,3…2,4)Fв. При дискретизации телефонных сигналов с диапазоном частот 0,3…3,4кГц частота дискретизации равна 8 кГц. При Fд>2Fв упрощаются требования к параметрам ФНЧ. ЗП — защитная полоса (полоса расфильтровки) |
Дата добавления: 2015-08-26; просмотров: 1358;
