Шифры замены
Шифры замены, или подстановки, являются самыми древними. В криптографии рассматриваются 4 типа замены: моноалфавитная, гомофоническая, полиалфавитная и полиграммная. При моноалфавитной заменекаждой букве алфавита открытого текста ставится в соответствие одна буква шифртекста из этого же алфавита. Приведем пример:
| а | б | в | г | д | е | ж | З |
| ф | ы | в | а | п | р | о | Л |
Тогда слово "багаж" будет заменено на слово "ыфафо". При расшифровании производится обратная операция.
Общая формула моноалфавитной замены выглядит следующим образом:
yi=k1xi+k2(mod n),
где yi – i-й символ алфавита; k1 и k2 – константы; xi – i-й символ открытого текста (номер буквы в алфавите); n – длина используемого алфавита.
Шифр, задаваемый формулой
yi=xi+ki(mod n),
где ki – i-я буква ключа, в качестве которого используется слово или фраза, называется шифром Вижинера.
Пример 2. Открытый текст: «ЗАМЕНА». Подстановка задана следующим образом:
| З | А | М | Е | Н | А |
| К | Л | Ю | Ч | К | Л |
y1= 8 + 11(mod 33) = 19 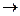 Т; y2=1 + 12(mod 33) = 13
Т; y2=1 + 12(mod 33) = 13 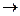 М;
М;
y3=13 + 31(mod ЗЗ) = 11 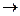 K; y4= 6 + 24(mod 33) = 30
K; y4= 6 + 24(mod 33) = 30 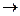 Э;
Э;
y5 = 14+ 11(mod 33) = 25 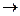 Щ; y6 = 1 + 12(mod 33) = 13
Щ; y6 = 1 + 12(mod 33) = 13 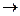 М.
М.
Шифртекст: «ТМКЭШМ».
Шифры Бофораиспользуют формулы:
уi = ki – xi(mod n) и уi =xi – ki(mod n).
Основным недостатком является то, что статистические свойства открытого текста (частоты повторения букв) сохраняются и в шифртексте. Формальный подход к дешифрованию основан на использовании средней частоты появления букв в текстах. Впервые похожий метод был предложен в конце 15-го века (итальянский математик Леон Баттиста Альберти) и использовал свойство неравномерности встречаемости разных букв алфавита. Позднее были определены средние частоты использования букв языка в текстах:
| Английский язык | Е (12,9) Т (9,7) А (8,0) I(7,5) N (7,0) R (7,0) O, S,, H, L, D, C, U, P, F, M, W, Y, B, G, V, K, Q, X, J, X |
| Немецкий язык | E(19,2) N (10,2) I (8,2) S (7,0) R (7,0) T (5,9) |
| Русский язык | O (11,0) И (8,9) Е (8,3) А (7,9) Н (6,9) Т (6,0) C, В, Р, Л, К, Д, М, П, У, Ы, Я, Б, Г, З, Ь, Ч, Х, Ж, Ш, Ю, Ц, Щ, Э, Ф |
Частота бyквосочетаний в английском языке:
TH, HE, IN, AN, EN, ER, OR, ES, ON, RE, AT, EA, ST, TI, ED, ND, NT, RR, LL, SS, MM.
QUI, ING, ION, ARE, TIO, ONE, ANT, MENT, TION, SION.
Частота бyквосочетаний в рyсском языке:
CТ, HО, ЕH, ТО, HА, ОВ, HИ, РА, ВО, КО, ОИ, ИИ, ИЕ, ЕИ, ОЕ, ИЯ, HH, CC.
CТО, ЕHО, HОВ, ТОВ, ОВО, HАЛ, РАЛ, HИC.
Кроме частоты появления букв, могут быть использованы другие обстоятельства, помогающие раскрыть сообщение. Например, может быть известна разбивка на слова и расставлены знаки препинания. Рассматривая сравнительно небольшое число возможных вариантов замены для предлогов и союзов, можно попытаться определить часть ключа. Использоваться может и то, какие буквы могут удвоены. Для искажения статистических свойств шифртекста применяются различные модификации.
Гомофоническая заменаодному символу открытого текста ставит всоответствие несколько символов шифртекста.
Пример 3. Открытый текст: «ЗАМЕНА». Подстановка задана следующей таблицей:
| Алфавит открытого текста | А | Б | ... | Е | Ж | З | ... | М | Н | ... |
| Алфавит шифротекста | ||||||||||
| ... | ... | ... | ||||||||
Шифртекст: «76 17 32 97 55 31» .
Таким образом, при гомофонической замене каждая буква открытого текста заменяется по очереди цифрами соответствующего столбца.
Полиграммная замена формируется из одного алфавита с помощью специальных правил. В качестве примера рассмотрим шифр Плэйфера. В этом шифре алфавит располагается в матрице. Открытый текст разбивается на пары символов xi,xi+1., икаждая пара заменяется на пару символов из матрицы следующим образом:
· если символы находятся в одной строке, то каждый из символов пары заменяется на стоящий правее его (за последним символом в строке следует первый);
· если символы находятся в одном столбце, то каждый символ пары заменяется на символ, расположенный ниже его в столбце (за последним нижним символом следует верхний);
· если символы пары находятся в разных строках и столбцах, то они считаются противоположными углами прямоугольника. Символ, находящийся в левом углу, заменяется на символ, стоящий в другом левом углу; замена символа, находящегося в правом углу, осуществляется аналогично;
· если в открытом тексте встречаются два одинаковых символа подряд, то перед шифрованием между ними вставляется специальный символ (например тире).
Пример 4. Открытый текст: «ШИФР ПЛЭЙФЕРА». Матрица алфавита представлена в следующей таблице. Шифртекст: «РДЫИ,– СТ – И.ХЧС».
| А | Ж | Б | М | Ц | В |
| Ч | Г | Н | Ш | Д | О |
| Е | Щ | , | Х | У | П |
| . | З | Ъ | Р | И | Й |
| С | Ь | К | Э | Т | Л |
| Ю | Я | _ | Ы | Ф | - |
При рассмотрении этих видов шифров становится очевидным, что чем больше длина ключа (например в шифре Вижинера), тем лучше шифр. Улучшения свойств шифртекста можно достигнуть при использовании шифров с автоключом.
Шифр, в котором сам открытый текст или получающаяся криптограмма используются в качестве ключа, называется шифром с автоключом. Шифрование в этом случае начинается с ключа, называемого первичным, и продолжается с помощью открытого текста или криптограммы, смещенной на длину первичного ключа.
Пример 5. Открытый текст: «ШИФРОВАНИЕ ЗАМЕНОЙ». Первичный ключ: «КЛЮЧ». Схема шифрования с автоключом при использовании открытого текста представлена в следующей таблице:
| Ш | И | Ф | Р | О | В | А | Н | И | Е | З | А | М | Е | Н | О | Й | |
| К | Л | Ю | Ч | Ш | И | Ф | Р | О | В | А | Н | И | Е | З | А | М | |
| В | Ф | Т | З | Ж | Л | Х | Ю | Ч | И | А | Х | Й | Т | Е | Х | П | Ц |
Схема шифрования с автоключом при использовании криптограммы представлена в следующей таблице:
| Ш | И | Ф | Р | О | В | А | Н | И | Е | З | А | М | Е | Н | О | Й | |
| К | Л | Ю | Ч | В | Ф | Т | З | С | Ч | У | Х | Ъ | Э | У | Э | Ы | Й |
| В | Ф | Т | З | С | Ч | У | Х | Ъ | Э | У | Э | Ы | Й | Щ | К | Й | У |
Для повышения стойкости шифра используют так называемые полиалфавитные подстановки, которые для замены используют несколько алфавитов шифротекста. Пусть имеется k алфавитов. Тогда открытый текст
X= x1x2 ...xkxk+1...x2kx2k+1...
заменяется шифротекстом
У =f1(x1)f2(x2)...fk(xk)f1(xk+1)...fk(x2k)f1(x2k+1)...,
где fi(xj) означает символ шифртекста алфавита i для символа открытого текста xj.
Пример 6. Открытый текст: «ЗАМЕНА», k = 3. Подстановка задана таблицей из примера 3. Шифртекст: «76 31 61 97 84 48».
Известно несколько разновидностей полиалфавитной подстановки, наиболее известными из которых являются одноконтурная (обыкновенная и монофоническая) и многоконтурная.
При полиалфавитной одноконтурной обыкновенной подстановке для замены символов исходного текста используются несколько алфавитов, причем смена алфавитов осуществляется последовательно и циклически, т.е. первый символ заменяется соответствующим символом первого алфавита, второй – символом второго алфавита и т. д. до тех пор, пока не будут использованы все выбранные алфавиты. После этого использование алфавитов повторяется.
В качестве примера рассмотрим шифрование с помощью таблицы Вижинера. Таблица Вижинера представляет собой квадратную матрицу с n2элементами, где n – число символов используемого алфавита. Ниже показана таблица Вижинера для русского языка. Каждая строка получена циклическим сдвигом алфавита на символ. Для шифрования выбирается буквенный ключ, в соответствии с которым формируется рабочая матрица шифрования. Осуществляется это следующим образом. Из полной таблицы выбирается первая строка и те строки, первые буквы которых соответствуют буквам ключа. Первой размещается первая строка, а под нею – строки, соответствующие буквам ключа в порядке следования этих букв в ключе.
| а | б | в | г | д | е | ж | з | . | ь | ъ | ы | э | ю | я |
| б | в | г | д | е | ж | з | и | . | ъ | ы | э | ю | я | а |
| в | г | д | е | ж | з | и | й | . | ы | э | ю | я | а | б |
| .. | .. | |||||||||||||
| я | а | б | в | г | д | е | ж | . | щ | ь | ъ | ы | э | ю |
Сам процесс шифрования осуществляется следующим образом:
1. под каждой буквой шифруемого теста записываются буквы ключа. Ключ при этом повторяется необходимое число раз;
2. каждая буква шифруемого текста заменяется по подматрице буквами, находящимися на пересечении линий, соединяющих буквы шифруемого текста в первой строке подматрицы и находящихся под ними букв ключа;
3. полученный текст может разбиваться на группы по несколько знаков.
Исследования показали, что при использовании такого метода статистические характеристики исходного текста практически не проявляются в зашифрованном сообщении. Нетрудновидеть, что замена по таблице Вижинера эквивалентна простой замене с циклическим изменением алфавита, т. е. здесь мы имеем полиалфавитную подстановку, причем число используемых алфавитов определяется числом букв в слове-ключе. Поэтому стойкость такой замены определяется произведением стойкости прямой замены на число используемых алфавитов, т. е. на число букв в ключе.
Расшифрование текста производится в следующей последовательности:
1. над буквами зашифрованного текста последовательно надписываются буквы ключа, причем ключ повторяется необходимое число раз;
2. в строке подматрицы Вижинера, соответствующей букве ключа отыскивается буква, соответствующая знаку зашифрованного текста. Находящаяся под ней буква первой строки подматрицы и будет буквой исходного текста;
3. полученный текст группируется в слова по смыслу.
Нетрудно видеть, что процедуры как прямого, так и обратного преобразований являются строго формальными, что позволяет реализовать их алгоритмически. Более того, обе процедуры легко реализуются по одному и тому же алгоритму.
Одним из недостатков шифрования по таблице Вижинера является то, что при небольшой длине ключа надежность шифрования остается невысокой, а формирование длинных ключей сопряжено с трудностями. Нецелесообразно выбирать ключ с повторяющимися буквами, так как при этом стойкость шифра не возрастает.
С целью повышения стойкости шифрования можно использовать усовершенствованные варианты таблицы Вижинера. Приведем некоторые из них:
1) во всех (кроме первой) строках таблицы буквы располагаются в произвольном порядке;
2) в качестве ключа используются случайные последовательности чисел. Из таблицы Вижинера выбираются десять произвольных строк, которые кодируются натуральными числами от 0 до 10. Эти строки используются в соответствии с чередованием цифр в выбранном ключе.
Частным случаем рассмотренной полиалфавитной замены является так называемая монофоническая замена. Особенность этого метода состоит в том, что количество и состав алфавитов выбираются таким образом, чтобы частоты появления всех символов в зашифрованном тексте были одинаковыми. При таком положении затрудняется криптоанализ зашифрованного текста с помощью его статистической обработки. Выравнивание частот появления символов достигается за счет того, что для часто встречающихся символов исходного текста предусматривается использование большего числа заменяющих элементов, чем для редко встречающихся. Шифрование осуществляется также, как и при простой замене (т. е. по шифрующему алфавиту № 1) с той лишь разницей, что после шифрования каждого знака соответствующий ему столбец алфавитов циклически сдвигается вверх на одну позицию. Таким образом, столбцы алфавита как бы образуют независимые друг от друга кольца, поворачиваемые вверх на один знак каждый раз после шифрования соответствующего знака. При увеличении объема текста частоты появления символов будут еще более выравниваться.
Полиалфавитная многоконтурная замена заключается в том, что для шифрования используется несколько наборов (контуров) алфавитов используемых циклически, причем каждый контур в общем случае имеет свой индивидуальный период применения. Этот период, исчисляется, как правило, количеством знаков, после зашифровки которых меняется контур алфавитов. Частным случаем многоконтурной полиалфавитной подстановки является замена по таблице Вижинера, если для шифрования используется несколько ключей, каждый из которых имеет свой период применения.
Общая модель шифрования подстановкой может быть представлена в следующем виде:
tiш= tiо +  mod(k -1),
mod(k -1),
где tiш – символ зашифрованного текста; tiо – символ исходного текста;  – целое число в диапазоне 0 – (k -1); k – число символов используемого алфавита.
– целое число в диапазоне 0 – (k -1); k – число символов используемого алфавита.
Если w фиксировано, то формула описывает моноалфавитную подстановку, если w выбирается из последовательности  1,
1,  2,...
2,...  n, то получается полиалфавитная подстановка с периодом n. Если в полиалфавитной подстановке n>m(где m – число знаков шифруемого текста) и любая последовательность
n, то получается полиалфавитная подстановка с периодом n. Если в полиалфавитной подстановке n>m(где m – число знаков шифруемого текста) и любая последовательность  1,
1,  2,...
2,...  n, используется только один раз, то такой шифр является теоретически нераскрываемым, если, конечно, злоумышленник не имеет доступа к исходному тексту. Такой шифр получил название шифра Вермэна и был предложен в 1917г. Нераскрываемым его считал сам изобретатель, но теоретически доказал лишь Шеннон.
n, используется только один раз, то такой шифр является теоретически нераскрываемым, если, конечно, злоумышленник не имеет доступа к исходному тексту. Такой шифр получил название шифра Вермэна и был предложен в 1917г. Нераскрываемым его считал сам изобретатель, но теоретически доказал лишь Шеннон.
Дата добавления: 2015-08-26; просмотров: 2310;
