Шифры перестановки
Этот метод заключается в том, что символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока символов, т.е. преобразования приводят к изменению только порядка следования символов исходного сообщения. Рассмотрим некоторые наиболее часто встречающиеся разновидности этого метода - простую, усложненную по таблице и усложненную по маршрутам перестановку.
Шифрование простой перестановкой (вертикальной перестановкой) осуществляется следующим образом:
1) выбирается ключевое слово с неповторяющимися символами;
2) шифруемый текст записывается последовательными строками под символами ключевого слова;
3) зашифрованный текст выписывается колонками в той последовательности, в которой располагаются в алфавите буквы ключа (или в порядке следования цифр в натуральном ряду, если ключ цифровой).
В качестве иллюстрации приведем пример шифрования способом простой перестановки сообщения: «БУДЬТЕ ОСТОРОЖНЫ С ПРЕДСТАВИТЕЛЕМ ФИРМЫ "ФЕНИКС". При этом применим цифровой ключ 5 – 8 – 1 – 3 – 7 – 4 – 6 – 2. В исходном тексте вместо пробелов используется буква а.
| Б | У | Д | Ь | Т | Е | а | О |
| С | Т | О | Р | О | Ж | Н | Ы |
| А | С | а | П | Р | Е | Д | С |
| Т | А | В | И | Т | Е | Л | Е |
| М | а | Ф | И | Р | М | Ы | а |
| Ф | Е | Н | И | К | С | а | а |
Выписывая текст по колонкам и группируя символы по пять, получаем зашифрованный текст в виде:
ДО  ВФ НОЫСЕ
ВФ НОЫСЕ  ЬРП ИИИЕЖ ЕЕМСБ С
ЬРП ИИИЕЖ ЕЕМСБ С  ТМФ
ТМФ  НДЛЫ
НДЛЫ  TOPT РКУТС A
TOPT РКУТС A  E
E  .
.
Расшифрование выполняется в следующем порядке:
1) подсчитываем число знаков в зашифрованном тексте и делим на число знаков ключа;
2) выписываем ключевое слово и под его знаками в соответствующей последовательности выписываем символы зашифрованного текста в определенном выше количестве;
3) по строкам таблицы читаем исходный текст.
Число ключей не более m!, где m - число столбцов таблицы.
Слабость шифрования простой перестановкой обуславливается тем, что при большой длине шифруемого текста в зашифрованном тексте могут проявиться закономерности символов ключа. Для устранения этого недостатка можно менять ключ после зашифровки определенного числа знаков. При достаточно частой смене ключа стойкость шифрования можно существенно повысить. При этом, однако, усложняется организация процесса шифрования и расшифрования.
Для получения и запоминания числового ключа существуют различные методы. Один из самых распространенных состоит в том, чтобы приписывать буквам числа в соответствии с алфавитным порядком букв. Возьмем, например, слово ПЕРЕСТАНОВКА. Присутствующая в нем буква А получает №1. Если какая-то буква входит несколько раз, то ее появления нумеруются последовательно слева направо. Поэтому второе вхождение буквы А получает №2. Буквы Б в этом слове нет, то буква В получает №3, и т.д.:
| П | Е | Р | Е | С | Т | А | Н | О | В | К | А |
Усложнение перестановки по таблице заключается в том, что для записи символов шифруемого текста используется специальная таблица, в которую введены некоторые усложняющие элементы. Усложнение состоит в том, что определенное число клеток таблицы не используется (на рисунке они пусты). Количество и расположение неиспользуемых элементов является дополнительным ключом шифрования. Шифруемый текст блоками по m х n – s элементов (m х n – размеры таблицы,s – число неиспользуемых элементов) записывается в таблицу. Далее шифрование аналогична простой перестановке.
| Б | У | Д | Ь | Т | Е | а | О | С | |
| Т | О | Р | О | Ж | Н | Ы | а | ||
| С | а | О | Р | Е | Д | С | Т | А | |
| В | И | Т | Е | Л | Е | М | а | Ф | |
| И | Р | М | Ы | а | Ф | Е | Н | И | |
| К | С | а | а | а | а | А | а | а |
Зашифрованный текст будет выглядеть так: ДОПР  БСВИК РРТМ
БСВИК РРТМ  ОЫ
ОЫ 
 Н
Н  ЕНСЕФ
ЕНСЕФ  УТ
УТ  И СС
И СС  АФ И
АФ И  ЬОЕ ЕЫ
ЬОЕ ЕЫ  Т МЕ
Т МЕ  ТЖ ДЛ
ТЖ ДЛ  .
.
При расшифровании знаки зашифрованного текста записываются столбцами таблицы в последовательности знаков ключа с пропуском неиспользуемых элементов. Исходный текст считывается по строкам. Варьируя размерами таблицы, последовательностью символов ключа, количеством и расположением неиспользуемых элементов, можно получить требуемую стойкость зашифрованного текста.
Еще один вариант - шифр "Поворотная решетка". предназначен для сообщений длины 4mk. Берется трафарет размером 2m*2k клеток, вырезается m*k клеток так, что при наложении его на лист бумаги того же размера 4 различными способами (поворачивая на 90°) его вырезы полностью покрывают всю площадь листа. Буквы сообщения последовательно вписываются в вырезы трафарета по строкам, в каждой строке слева направо, при каждом из 4-х его возможных положений в заранее установленном порядке. Число возможных трафаретов, т.е. количество ключей этого шифра составляет 4mk (при размере трафарета 8*8 число вариантов превосходит 4 миллиарда).
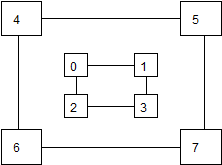
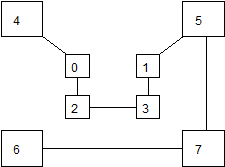
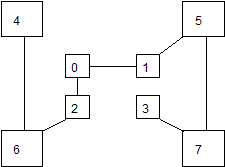
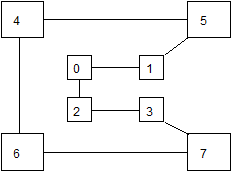
Весьма высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских. При этом для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используется несколько различных маршрутов. Для примера рассмотрим шифрование по маршругам Гамильтона при n =3. Структура и три маршрута показаны на Рис. 7, а пример шифрования – на Рис. 8.
Шифруемый текст: БУДЬТЕ ОСТОРОЖНЫ С ПРЕДСТАВИТЕЛЕМ ФИРМЫ ФЕНИКС
Зашифрованный текст: ТЕУБД ЬОаОС ОРТЖЫ НЕСПа ...
|
|
|
|
Рис. 7 Пример структуры и маршрутов Гамильтона
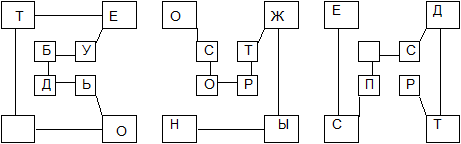
Рис. 8 Пример шифрования по маршрутам Гамильтона
В 1991 г. В.М. Кузьмич предложил схему перестановки, основанную на кубике Рубика. Согласно этой схеме открытый текст записывается в ячейки граней куба по строкам. После осуществления заданного числа заданных поворотов слоев куба считывание шифртекста осуществляется по столбцам. Сложность расшифрования в этом случае определяется количеством ячеек на гранях куба и сложностью выполненных поворотов слоев. Перестановка, основанная на кубике Рубика, получила название объемной (многомерной) перестановки. В 1992 – 94 гг. идея применения объемной перестановки для шифрования открытого текста получила дальнейшее развитие. Усовершенствованная схема перестановок по принципу кубика Рубика, в которой наряду с открытым текстом перестановке подвергаются и функциональные элементы самого алгоритма шифрования, легла в основу системы «Рубикон». В качестве прообразов пространственных многомерных структур, на основании объемных преобразований которых осуществляются перестановки, в ней используются трехмерный куб и тетраэдр.
Дата добавления: 2015-08-26; просмотров: 7277;
