Шифрование с помощью аналитических преобразований.

Достаточно надежное закрытие информации может быть обеспечено при использовании для шифрования некоторых аналитических преобразований. Для этого можно использовать методы алгебры матриц, например, умножение матрицы на вектор по правилу ||a_ij||b_j =c_{j = .}

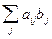Если матрицу ||a_ij|| использовать в качестве ключа, а вместо компонента вектора b_jподставить символы исходного текста, то компоненты вектора с_j будут представлять собой символы зашифрованного текста.

Приведем пример использования такого метода, взяв в качестве ключа квадратную матрицу третьего порядка

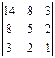
Заменим буквы алфавита цифрами, соответствующими их порядковому номеру в алфавите: А-О, Б-1, В-2, и т.д. Тогда отрывку текста ВАТАЛА... (текст взят произвольно) будет соответствовать последовательность 3, 0, 19, 0, 12, 0. По принятому алгоритму шифрования выполним необходимые действия:

* =

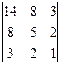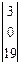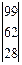
При этом зашифрованный текст будет иметь вид: 99, 62, 28, 96, 60, 24.

Расшифрование осуществляется с использованием того же правила умножения матрицы на вектор, только в качестве основы берется матрица, обратная той, с помощью которой осуществляется закрытие, а в качестве вектора-сомножителя – соответствующее количество символов закрытого текста; тогда значениями вектора-результата будут цифровые эквиваленты знаков открытоготекста. Матрица, обратная к принятой нами за основу для закрытия, будет иметь вид

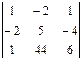
Тогда в условиях нашего примера процесс раскрытия будет выглядеть так:

* = =

* = = .

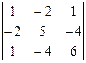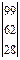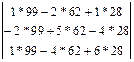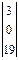
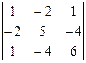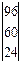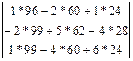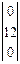Таким образом, получили следующую последовательность знаков раскрытого текста: 3; 0; 19; 0; 12; 0; ..., что соответствует исходному тексту. Нетрудно видеть, что и этот метод шифрования является формализованным, что позволяет легко реализовать его программными средствами.