Уравнения линейного трансформатора.

Пусть i₁, i₂ — мгновенные значения тока в первичной и вторичной обмотке соответственно, u₁ — мгновенное напряжение на первичной обмотке, R_H — сопротивление нагрузки. Тогда

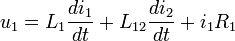
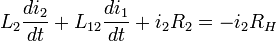
Здесь L₁, R₁— индуктивность и активное сопротивление первичной обмотки, L₂, R₂— то же самое для вторичной обмотки, L₁₂— взаимная индуктивность обмоток. Если магнитный поток первичной обмотки полностью пронизывает вторичную, то есть если отсутствует поле рассеяния, то 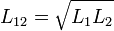. Индуктивности обмоток в первом приближении пропорциональны квадрату количества витков в них.

Мы получили систему линейных дифференциальных уравнений для токов в обмотках. Можно преобразовать эти дифференциальные уравнения в обычные алгебраические, если воспользоваться методом комплексных амплитуд.

Для этого рассмотрим отклик системы на синусоидальный сигнал u₁=U₁ e^{-jω t} (ω=2π f, где f — частота сигнала, j — мнимая единица). Тогда i₁=I₁ e^{-jω t} и т. д., сокращая экспоненциальные множители получим

U₁=-jωL₁ I₁ -jωL₁₂ I₂+I₁ R₁

-jωL₂ I₂ -jω L₁₂ I₁+I₂ R₂ =-I₂ Z_н

Метод комплексных амплитуд позволяет исследовать не только чисто активную, но и произвольную нагрузку, при этом достаточно заменить сопротивление нагрузки R_н еёимпедансом Z_н. Из полученных линейных уравнений можно легко выразить ток через нагрузку, воспользовавшись законом Ома— напряжение на нагрузке, и т. п.