Уравнения идеального трансформатора
Идеальный трансформатор — трансформатор, у которого отсутствуют потери энергии на нагрев обмоток и потоки рассеяния обмоток. В идеальном трансформаторе все силовые линии проходят через все витки обеих обмоток, и поскольку изменяющееся магнитное поле порождает одну и ту же ЭДС в каждом витке, суммарная ЭДС, индуцируемая в обмотке, пропорциональна полному числу её витков. Такой трансформатор всю поступающую энергию из первичной цепи трансформирует в магнитное поле и, затем, в энергию вторичной цепи. В этом случае поступающая энергия равна преобразованной энергии:
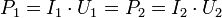
Где
P1 — мгновенное значение поступающей на трансформатор мощности, поступающей из первичной цепи,
P2 — мгновенное значение преобразованной трансформатором мощности, поступающей во вторичную цепь.
Соединив это уравнение с отношением напряжений на концах обмоток, получим уравнение идеального трансформатора:
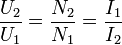
Таким образом получаем, что при увеличении напряжения на концах вторичной обмотки U2, уменьшается ток вторичной цепи I2.
Для преобразования сопротивления одной цепи к сопротивлению другой, нужно умножить величину на квадрат отношения. Например, сопротивление Z2 подключено к концам вторичной обмотки, его приведённое значение к первичной цепи будет 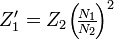 . Данное правило справедливо также и для вторичной цепи:
. Данное правило справедливо также и для вторичной цепи: 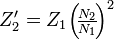 .
.
Дата добавления: 2015-08-26; просмотров: 1553;
