Тема 21 Уравнение Бернулли для потока конечных размеров. Гидравлический и пьезометрический уклоны

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме давлений имеет вид:

r × g × z + р + r × a × 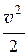= const, (21.1, а)

где r × g × z – гравитационное давление;

р – статическое давление;

r × 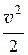– динамическое давление.

Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:

r × g × z₁ + р₁ + r × a₁ × 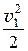= r × g × z₂ + р₂ + r × a₂ × 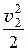= const. (21.1, б)

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме напоров имеет вид:

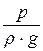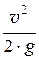z + + a× = Н = const, (21.2, а)

где z – удельная потенциальная энергия положения;

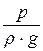– удельная потенциальная энергия давления;

a × 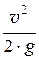– удельная кинетическая энергия (динамический напор для потока);

Н – полная удельная энергия потока.

Таким образом, полная удельная энергия потока есть сумма удельной потенциальной энергии 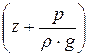и удельной кинетической энергии a × .

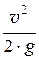Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:

z₁ + 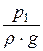+ a₁ × 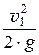= z₂ + 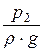+ a₂ × 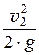= Н = const. (21.2, б)

С энергетической точки зрения уравнение Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма удельных энергий – потенциальной (положения и давления) и кинетической – есть величина постоянная.

Все члены уравнения Бернулли имеют линейную размерность и их можно интерпретировать как высоты:

z – геометрическая высота, то есть высота положения рассматриваемой точки пространства с жидкостью (центра тяжести сечения) над горизонтальной плоскостью сравнения x0y;

Если в уравнении Бернулли:

· р – абсолютное (полное) давление, то величина 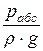= 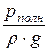– высота давления;

· р – избыточное (манометрическое) давление, то величина 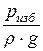= 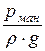называется пьезометрической высотой;

a × 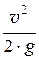– скоростная (или динамическая) высота.

Н = 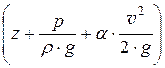– полная высота в данном сечении потока.

Таким образом, геометрический смысл уравнения Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма высот – положения, давления (или пьезометрической) и скоростной – есть величина постоянная.

В потоке скорости в разных точках поперечного сечения различны, а скоростной напор, определяемый средней скоростью v, дополнен коэффициентом кинетической энергии (или коэффициентом Кориолиса) a. Величина этого коэффициента отражает степень неравномерности распределения скоростей по сечению потока. Коэффициент равен отношению истинной кинетической энергии массы жидкости, протекающей через живое сечение, к кинетической энергии, вычисленной в предположении, что во всех точках живого сечения местные скорости равны средней скорости.

Обычно при прямолинейном турбулентном движении в трубах a = 1,03…1,1. Обычно при расчётах при турбулентном течении в трубах принимают коэффициент Кориолиса a равным 1,1 или 1. При прямолинейном ламинарном движении в трубах a = 2.

При движении реальной (вязкой) жидкости часть механической энергии теряется (переходит в тепловую).

Уравнение Бернулли для установившегося движения вязкой несжимаемой жидкости между двумя сечениями имеет вид:

· в форме давлений

r × g × z₁ + р₁ + r × a₁ × 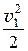= r × g × z₂ + р₂ + r × a₂× 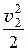+ Dр, (21.3)

где Dр – потери давления на участке между рассматриваемыми сечениями;

· в форме напоров

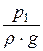z₁ + + a₁× 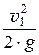= z₂ + 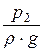+ a₂ × 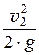+ Dh_пот, (21.4)

z_i + 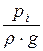+ a_i × 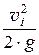+ D 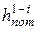= Н = const.

где Dh_пот – потери напора на участке между рассматриваемыми сечениями.

Для потока жидкости сумма удельной потенциальной и удельной кинетической энергии

Н = 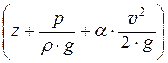(21.5)

называется гидродинамическим (или полным) напором.

При движении вязкой жидкости линия удельной энергии (напорная линия) не горизонтальна, как при движении невязкой жидкости, а представляет собой наклонную линию, так как удельная энергия потока (гидродинамический напор) Е = Н = 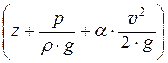при движении вязкой жидкости уменьшается в направлении движения.

Энергетический смысл уравнения Бернулли для потока вязкой жидкости:

удельная энергия потока в предыдущем сечении всегда больше чем в последующем на величину потерь удельной энергии.

Геометрический смысл уравнения Бернулли для потока вязкой жидкости:

полная высота в предыдущем сечении всегда больше чем в последующем на высоту потерь Dh_пот.

Гидравлическим уклоном i называется отношение потерь напора Dh_потк длине участка l, на котором эти потери происходят:

i = 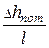= 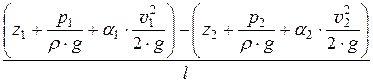> 0. (21.6, а)

Так как напор уменьшается вдоль движения, то гидравлический уклон всегда положителен.

Удельная потенциальная энергия 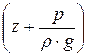(пьезометрический напор) в направлении движения может, и уменьшатся, и увеличиваться, в зависимости от конкретных условий.

Пьезометрическим уклоном i_п называется отнесённое к единице длины изменение пьезометрического напора 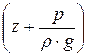или изменение отметок пьезометрической линии.

Для двух сечений имеем

i_п = 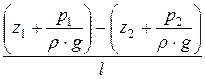. (21.7, б)

Пьезометрический уклон может быть положительным, отрицательным и равным нулю. Пьезометрический уклон считается положительным, если по течению пьезометрическая линия понижается.