Стационарное уравнение Шредингера.

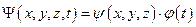(ищем решение в таком виде).

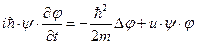
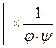
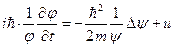
Примечание:

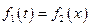только если .

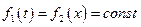Обозначим .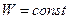

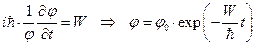
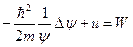
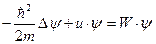- стационарное уравнение Шредингера.

Оно стационарно, если:

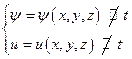(значок 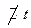означает независимость от ).

.

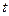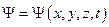В стационарном случае , .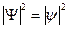

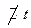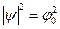Операторная форма:

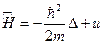
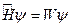
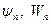- решения.

Пример 1. (свободная частица массой 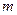, движущаяся со скоростью 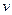вдоль оси ).

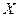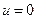(свободная частица, нет внешнего силового поля).

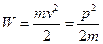
(так как движение происходит только вдоль оси )

.

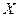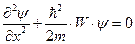
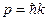
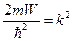
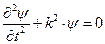
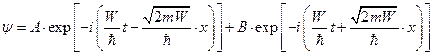
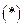Общее решение- две плоские волны вдоль и вдоль .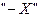

В нашем случае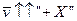

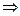
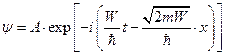
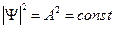- полная неопределенность координаты и полная ясность с импульсом .

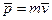Пример 2.(электрон в потенциальном «ящике» (яме, колодце) ).

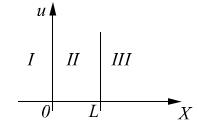
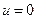, если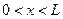

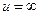, если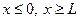

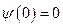, - граничные условия.