Соотношение неопределенностей Гейзенберга. - неопределенность координаты
Для любых волн 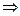 1).
1). 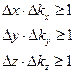
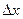 - неопределенность координаты
- неопределенность координаты 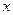
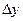 - неопределенность координаты
- неопределенность координаты 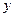
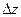 - неопределенность координаты
- неопределенность координаты 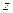
2). 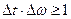
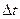 - временная неопределенность.
- временная неопределенность.
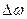 - частотная неопределенность.
- частотная неопределенность.
Для волн де Бройля: 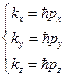
1). 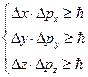
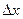 ,
, 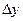 ,
, 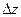 - неопределенности координат.
- неопределенности координат.
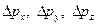 - неопределенности краевых импульсов.
- неопределенности краевых импульсов. 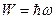
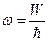
2). 
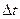 - временная неопределенность.
- временная неопределенность.
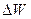 - неопределенность энергии.
- неопределенность энергии.
Пример 1. (Пылинка).
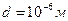
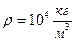
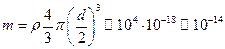
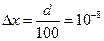
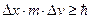
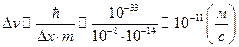 .
.
В макромире можно пользоваться понятием траектории.
Пример 2.(Электрон в атоме).
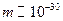
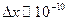
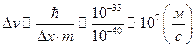
Метод, который используется в классической механике, не работает при расчете траектории.
Основным уравнением квантовой волновой механики является дифференциальное уравнение для волновой функции.
Уравнение Шредингера (1926 г.) 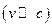
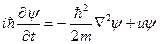
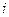 - «мнимая единица» (
- «мнимая единица» (  )
)
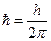 - постоянная Планка.
- постоянная Планка.
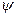 - нестационарная волновая функция.
- нестационарная волновая функция.

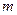 - масса частицы.
- масса частицы.
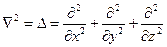
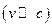
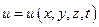 - потенциальная энергия частицы.
- потенциальная энергия частицы.
27.11.06.
«Вывод» уравнения Шредингера.
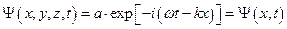
Плоская волна, вдоль оси 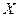 .
.
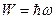 ,
, 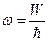 ,
, 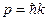 ,
, 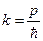
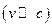
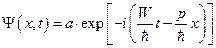
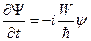 ,
, 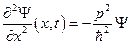
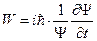 ,
, 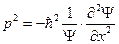
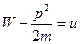 , где
, где 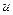 - потенциальная энергия.
- потенциальная энергия.
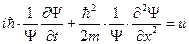

Обобщаем 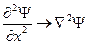
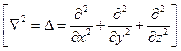
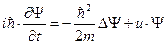 - временное уравнение Шредингера (временное, так как в него
- временное уравнение Шредингера (временное, так как в него
входит полная волновая функция 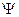 .
.
Дата добавления: 2015-08-26; просмотров: 833;
