Понятие о термодинамических потенциалах

Наряду с энтропией используют ряд других, связанных с ней функций состояния системы. Наиболее важны из них:

1. 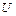– внутренняя энергия;

2. 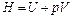– энтальпия;

3. 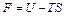– свободная энергия (функция Гельмгольца);

4. 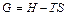– функция Гиббса.

Данные функции состояния являются термодинамическими потенциалами. Это следует из того, что при равновесных процессах, в которых остаются постоянными некоторые из параметров системы, убыль термодинамических потенциалов равна совершаемой системой работе.

Покажем это, используя первое начало термодинамики .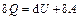

1. Внутренняя энергия .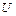

При адиабатическом процессе 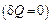имеем: .

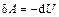2. Энтальпия .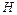

В самом общем случае совершаемую системой элементарную работу 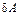можно представить в виде:

,

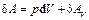где 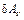– работа, не связанная с изменением объема системы (например, работа против сил поверхностного натяжения, работа по перемещению зарядов в электрическом поле и т.д.).

Тогда первое начало имеет вид:

.

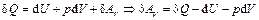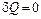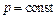Отсюда при одновременном выполнении условий и получим:

.

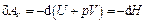3. Свободная энергия .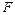

Для обратимых процессов: .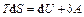

При 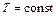получим: .

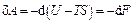Тогда 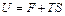, т.е. внутреннюю энергию системы можно разделить на две части. Одна из них – свободная энергия – может быть превращена в работу при обратимом изотермическом процессе и в этом смысле является «свободной». Вторая, равная 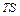, в том же процессе не может быть превращена в работу и называется связанной энергией.

Для термодинамической системы, находящейся при постоянных температуре и объеме, 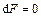. При необратимом процессе 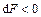, т.е. свободная энергия может только убывать, поэтому условием равновесия такой системы будет условие минимума свободной энергии.

4. Функция Гиббса .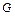

С учетом работы, не связанной с изменением объема системы:

.

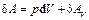Тогда .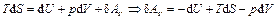

Отсюда пр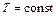и и 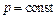имеем:

.

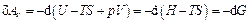Зависимость давления насыщенного пара

от температуры

Чтобы проинтегрировать уравнение Клапейрона-Клаузиуса, найдём сначала зависимость теплоты испарения от температуры, т.е. L(T).

К состоянию пара при температуре Т от жидкости при температуре Т₀ можно прийти двумя путями.

1-ый способ: испарить жидкость при температуре Т₀ и нагреть пар при постоянном давлении до температуры Т. Затрачиваемая на 1 моль энергия равна:

2-ой способ: жидкость нагреть до Т, а затем испарить.

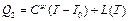
Начальные и конечные состояния в обоих способах одинаковы, поэтому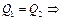

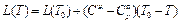
В уравнении Клапейрона-Клаузиуса можно пренебречь молярным объёмом жидкости по сравнению с молярным объёмом газа:

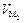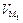« , где .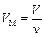

Кроме того, для пара предполагаем выполнение уравнения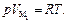

Тогда .

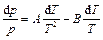Таким образом, давление насыщенного пара для фазового перехода жидкость–газ определяется формулой:

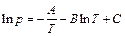, где А, B, С – постоянные.