Падение и потеря напряжения в линии
Различие в напряжениях U2ф и U1ф в П-образной схеме определяется падением напряжения на сопротивлении Z12 (Z12+jx12), вызванным током I12. Определяется это падением напряжения как сумма вектора I12r12, совпадающего по фазе с вектором I12 и вектора I12´jx12, опережающего вектор I12 на 90о.
Падение напряжения – геометрическая (векторная) разность между комплексами напряжений начала и конца линий.
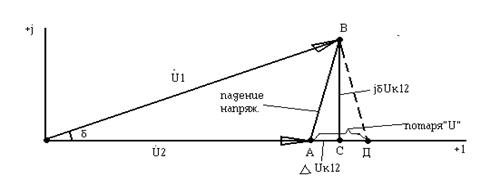 |
На рис. падение напряжения это вектор
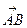 , т.е.
, т.е. 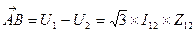
разность комплексных значений по концам линий, используется для характеристики режима линии.
Продольной составляющей падения напряжения DUк12 называют проекцию падения напряжения на действительную ось или на напряжение U2, DUк12=АС. Индекс “к” означает , что Uк12 – проекция на напряжение конца линии U2.
Обычно DUк12 выражается через данные в конце линии: U2, Pк12, Qк12.
Поперечная составляющая падения напряжения dUк12 – это проекция падения напряжения на мнимую ось, jdUк12=СВ. Т. о. U1-U2=  ´I12´Z12=DUк12+jdUк12.
´I12´Z12=DUк12+jdUк12.
Величина dUк12 определяет сдвиг вектора напряжения в начале линии (U1) на угол d по отношению к вектору напряжения в ее конце (U2).
Часто используют понятие потеря напряжения – это алгебраическая разность между модулями напряжений начала (U1) и конца (U2) линий.
На рис. çU1ê– êU2ê=АД.
Если поперечная составляющая dUк12 мала (например, в сетях Uном £ 110кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения напряжения.
Потеря напряжения является показателем изменения относительных условий работы потребителей в начале и в конце линии.
Расчет режимов линий электропередач и электрических сетей
при заданной мощности нагрузки
При подаче энергии по линии от начала к ее концу имеют место потери реактивной мощности. Они обусловлены реактивным сопротивлением линии и соответствующим ему реактивным сопротивлением схемы замещения этой линии. При передаче энергии имеют место и потери активной мощности, расходуемой на нагревание проводов. Поэтому в схеме замещения следует различать полную мощность до сопротивления Z12(r12+jx12), Sн12 и после него Sк12.
Расчет режима ЛЭП при заданной мощности нагрузки и напряжении
в конце линии
Задано напряжение в конце линии U2=сonst. Известна мощность нагрузки S2, напряжение U2, сопротивление и проводимость линии Z12=r12+jx12, в12.
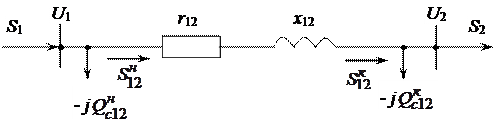 |
Необходимо определить напряжение U1, мощности в конце и в начале продольной части линии Sк12, Sн12, потери мощности DS12, мощность в начале линии S1. Для проверки ограничений по нагреву иногда определяют ток в линии I12.
Расчет аналогичен расчету при заданном токе нагрузке (I2), и состоит в последовательном определении от конца линии к началу неизвестных мощностей и напряжений при использовании I закона Кирхгофа и закона Ома. Будем использовать мощности трех фаз и линейные напряжения.
Зарядная (емкостная) мощность трех фаз в конце линии:
–jQкс12=3I*кс12´U2ф= 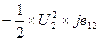
Мощность в конце продольной части линии по I закону Кирхгофа: Sк12=S2 – jQкс12
Потери мощности в линии: DS12=3I212Z12= 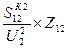
Ток в начале и в конце продольной ветви линии одинаков.
Мощность в начале продольной ветви линии больше, чем мощность в конце, на величину потерь мощности в линии, т.е. Sн12=Sк12+DS12
Линейное напряжение в начале линии по закону Ома равно:
U1=U2+  I12Z12=U2+
I12Z12=U2+ 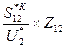
Емкостная мощность в начале линии: -jQнc12= 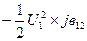
Мощность в начале линии: S1=Sн12 – jQнс12
Под влиянием зарядной мощности Qс реактивная мощность нагрузки Q2 в конце, схема замещения уменьшается. Аналогичное явление имеет место и в начале схемы замещения, где реактивная мощность Qс уменьшает реактивную мощность в начале линии.
Это свидетельствует о том, что зарядная мощность сокращает реактивную мощность, поступающую от станции в линию для питания нагрузки. Поэтому зарядная мощность условно может рассматриваться как “генератор” реактивной мощности.
В линии электрической сети имеют место как потери, так и генерация реактивной мощности.
От соотношения потерь и генерации реактивной мощности зависит различие между реактивными мощностями в начале и конце линии.
Расчет режима ЛЭП при заданной мощности нагрузки и напряжении
в начале линии
Задано напряжение в начале линии.
Схема замещения:
 |
U1=сonst. Известны S2, U1 ,Z12=r12+jx12, в12.
Необходимо определить U2, Sк12, Sн12, DS12, S1
Т.к. U2 неизвестно, то невозможно определить последовательно от конца линии к началу определить неизвестные токи и напряжения по I закону Кирхгофа и закону Ома.
Дата добавления: 2015-08-21; просмотров: 2365;
