Режимы и параметры системы и сети
Состояние системы в любой момент времени или на некотором интервале времени называется режимом системы.
Режим определяется показателями, которые называются параметрами режима к их числу относятся:
1)частота,
2)активная и реактивная мощность в элементах системы,
3)напряжение в различных точках сети у потребителей,
4)величины токов,
5)величины углов расхождения векторов ЭДС и напряжения.
Различают три основных вида режимов электроэнергетических систем:
1. Нормальный установившейся режим, применительно к которому проектируется элкктрическая сеть и определяются ее технико–экономические характеристики;
2. Послеаварийный установившийся режим, наступающий после аварийного отключения какого – либо элемента сети или ряда элементов (в этом режиме система и соответственно сеть могут работать с несколько ухудшенными технико– экономическими характеристиками);
3. Переходный режим, во время которого система переходит из одного состояния к другому.
Любой режим состоит из множества различных процессов.
Различают параметры режима и параметры сети.
Параметры режима электрической сети связаны между собой определенными зависимостями, в которые входят некоторые коэффициенты, зависящие от физических свойств элементов сети, от способа соединения этих элементов между собой, а также от некоторых допущений расчетного характера.
К ним относятся полное сопротивление, активное и реактивное сопротивление, проводимости элементов, собственная и взаимная проводимости, коэффициент трансформации, коэффициент усиления.
Например, ток на участке ЛЭП определяется зависимостью: I= 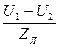 ; Здесь U1,U2,I – параметры режима; ZЛ – сопротивление данного участка системы (линии), является одним из параметров сети.
; Здесь U1,U2,I – параметры режима; ZЛ – сопротивление данного участка системы (линии), является одним из параметров сети.
Ряд параметров сети зависит от характера изменений ее режима, т.е. является нелинейной системой. Однако во многих практических задачах параметры сети можно полагать не изменяющимися и считать сеть линейной.
Другой вид нелинейности сети обусловлен характером соотношений между параметрами ее режима. Так, мощность, связана квадратичной зависимостью с напряжением и т.д.( S=  ´U´I=
´U´I=  ´U´
´U´ 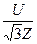 =
= 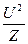 )
)
Нелинейность такого вида надо учитывать.
Электрическую сеть рассматривают применительно к неизменному режиму системы, но в действительности такого режима не существует, и говоря об установившемся режиме имеют в виду режим малых возмущений. Отклонения параметров режима, происходит около некоторого устойчивого состояния.
Система должна быть устойчива при этих малых возмущениях. Иначе говоря, она должна обладать статической устойчивостью.
Аварийные переходные процессы возникают при резких аварийных изменениях режима, например, при к.з. элементов системы и последующем их отключении, при изменении схемы электрических соединений элементов системы.
Большие возмущения в системе при аварийных переходных процессах приводят к значительным отклонениям параметров режима к большим возмущениям, устойчивость по отношению к которым определяют как динамическую.
При этом под динамической устойчивостью понимают способность системы восстанавливать после больших возмущений свое состояние, практически близкое к исходному.
Необходимо учитывать изменения параметров режима, которые возникают при 1)увеличении передаваемых мощностей, 2)росте нагрузок и 3)изменении схемы электрических соединений в результате повреждений в сети.
Расчет режимов линий электропередач и электрических сетей
Связь между изменяющимися величинами определяется с помощью диаграмм, в которых каждая из величин характеризуется вектором. Построим диаграмму, показывающую соотношения между токами и напряжениями П-образной схемы замещения.
Расчет режима ЛЭП при заданном токе нагрузки и напряжении
в конце линии
Будем считать, что режим конца линии задан фазным напряжением Uф=сonst и отстающим током нагрузки I2. Также заданы Z12=r12+jx12, в12.
Необходимо определить 1) напряжение в начале линии – U1,2) ток в продольной части – I12, 3) потери мощности - DS12 4) ток в начале линии – I1.
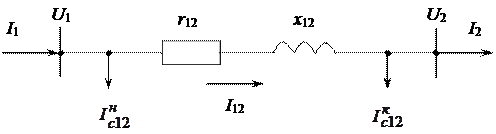 |
Расчет состоит в определении неизвестных токов и напряжений, последовательно от конца линии к началу.
Емкостный ток в конце линии 1-2, по закону Ома:
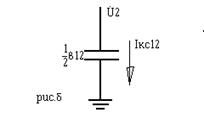 |
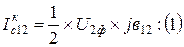
Ток в продольной части линии 1-2, по первому закону Кирхгофа: I12=I2+Iкс12: (2)
Напряжение в начале линии по закону Ома: U1ф=U2ф+I12´Z12: (3)
Емкостный ток в начале линии: 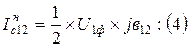
Ток в начале линии по первому закону Кирхгофа: 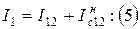
Потери мощности в линии (в трех фазах): DS12=3I212´Z12: (6)
Векторная диаграмма токов и напряжений строится в соответствии с выражениями 1-5.
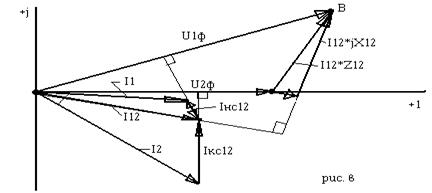 |
Вначале строим известные U2ф и I2.
Полагаем что U2ф=U2ф, т.е. напряжение U2ф направлено по действительной оси. Емкостный ток 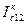 опережает на 90о напряжение U2ф. Ток I12 соединяет начало первого и конец второго суммируеммых векторов в правой части урав.(2) [I12=I2+
опережает на 90о напряжение U2ф. Ток I12 соединяет начало первого и конец второго суммируеммых векторов в правой части урав.(2) [I12=I2+ 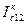 ]
]
Затем строим отдельно два слагаемых в правой части (3) [U1ф=U2ф+I12´Z12]. I12´Z12=I12´r12+I12´jx12 (7)
Вектор I12´r12 êê I12, вектор I12´jx12 опережает на 90о ток I12
Напряжение U1ф соединяет начало и конец суммируемых векторов U2ф, I12´r12, I12´jx12.
Ток  опережает U1ф на 90о.
опережает U1ф на 90о.
I1 соответствует (5) I1=I12+ 
В линии с нагрузкой напряжение в конце линии по модулю меньше, чем в начале U2ф<U1ф.
На линии на холостом ходу (I2=0), течет только емкостной ток, т.к. в соответствии с формулой I12=I2+Iкс12 (2) I12=Iкс12
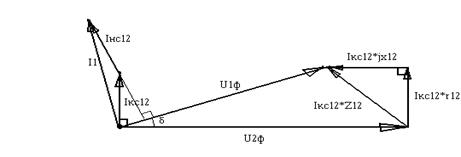 |
В этом случае напряжение в конце линии повышается U2ф>U1ф
Векторная диаграмма для такой линии:
Дата добавления: 2015-08-21; просмотров: 866;
