Фотон и его основные свойства
 |  |  |
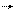
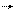
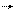
 Энергия фотона E = hn = hw. h = h/(2p), где h – это постоянная Планка и h = 1,05 Дж*с. Фотону свойственен импульс. p = hk, где k = (2p/l). k – волновой вектор.
Энергия фотона E = hn = hw. h = h/(2p), где h – это постоянная Планка и h = 1,05 Дж*с. Фотону свойственен импульс. p = hk, где k = (2p/l). k – волновой вектор.
Электрон
Масса m = 9,1*10-31 кг. Заряд электрона e = 1,6*10-19 Кл. Так же как и фотон электрон обладает импульсом.
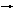 k = p/t
k = p/t
 длина волны электрона l = 2ph/p
длина волны электрона l = 2ph/p
 2p/l = p/h
2p/l = p/h
Чтобы описать волновые свойства нужно ввести волновую функцию. Эта волновая функция y(x,y,z,t). |y(x,y,z,t)|2 – вероятность обнаружить частицу в данной точке пространства в данный момент времени. Существенным свойством такого квантового описания является его вероятностный характер. Т. е. о том, что определенная система находится в том или ином состоянии можно говорить только с определенной долей вероятности.
Рассмотрим несколько примеров систем.
У этой волновой функции есть свойство суперпозиции:
y = y1 + y2
Если система может находиться в каких-то нескольких состояниях, то ее общее состояние может описываться на основе сумы волновых функций, которыми обладает система. Проиллюстрируем это.
Пример 1: свободная частица, о которой мы знаем, что она имеет импульс p0. В соответствии с формулой мы можем приписать ее вполне определенную длину волны:
 l0 = 2ph/p0
l0 = 2ph/p0
Известно, что волна, длина которой не меняется, это монохроматическая волна. Про координаты этой частицы мы ничего не знаем. Попробуем найти волновую функцию этой частицы. Поскольку это волна, то можно считать, что волновая функция должна изменятся по закону синуса или косинуса y = Acos(k0x – wt), где А – какой-то коэффициент. Тогда вероятность нахождения частицы |y|2 = A2cos2(…). Эта функция содержит нули и нам не подходит потому, что свободная частица равновероятна в любой точке. Подходит такая функция y = Aei(k0x – wt). Эта волновая функция комплексная: |y|2 = y**y = A2.
Пример 2:
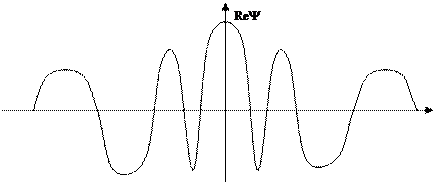 |
 Зададим распределение волновой функции только на конечном участке.
Зададим распределение волновой функции только на конечном участке.
y(x) = Ae *eikox
А – амплитуда. Это гармоническая функция. Амплитуда по х ограничена sx. Это известное Гауссово распределение. С вероятностью 50 % она находится вблизи точки х = 0. Мы знаем, что по х она находится в пределах от –sx до +sx. Что мы знаем о скорости этой частицы или о ее импульсе? Разложим волновую функцию в интеграл Фурье.
 |
y(x) = B(k)eikxdk
Найдем коэффициенты разложения
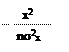 | |||||||
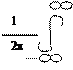 | 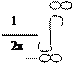 | 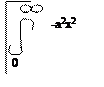 | |||||
B(k) = y(x)e-ikxdx = Ae * e-i(k-k0)xdx = e cosmxdx =
 | |||||||
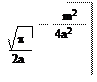 |  | ||||||
| |||||||
|
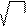
 e = A e
e = A e
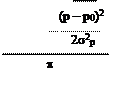
A2s2xe = |B(p)|2
Оказывается, что импульс тоже распределен по закону Гаусса:
 sp = h/2sx
sp = h/2sx




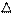
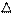 spsx = p x = h/2 - это в случае распределения Гаусса. А в случае любого другого распределения будет p x > h/2. Это так называемое соотношение неопределенности, которое означает, что чем точней мы мерим координату, тем меньше мы знаем об импульсе и о скорости и наоборот. Это соотношение можно преобразовать в следующее:
spsx = p x = h/2 - это в случае распределения Гаусса. А в случае любого другого распределения будет p x > h/2. Это так называемое соотношение неопределенности, которое означает, что чем точней мы мерим координату, тем меньше мы знаем об импульсе и о скорости и наоборот. Это соотношение можно преобразовать в следующее:

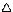
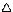
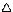
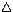
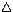
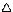
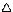
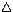 p x = m v * v t = mv v t = E t > h/2
p x = m v * v t = mv v t = E t > h/2
Электрон характеризуется таким образом: чем мы больше хотим о нем знать с какой-то его одной стороны, тем меньше о нем знаем с другой, а в целом никогда ничего не можем сказать определенного.
Пример 3. Помещаем электрон в ящик с бесконечными стенками, т.е. если мы туда электрон забросим, то он там и будет. Мы не знаем, что с ним происходит, но точно знаем, что он там. Попытаемся объяснить, что с ним там происходит. Электрон в атоме водорода притягивается к протону и не отрывается от него – аналогия.

За стенки электрон выйти не может. Абсолютно достоверно можно утверждать, что электрон в ящике покоиться не может. Доказательство этого утверждения: если бы он там покоился, тогда можно было бы сказать, что у него импульс равен 0, т.е. вполне определенный импульс, а значит, он размазан по пространству. А он в ящике – он не может быть размазан. Т.е. он там движется. С ним соотносится волновая функция. Вероятность распределения электрона за пределы этого ящика равна 0. То естественно здесь должно оказываться либо пол волны, либо целая волна, либо 3 полу периода длины волны. Вероятность распределения должна быть непрерывна. Мы можем утверждать, что длина волны может иметь только строго определенные значения. А раз длина волны дискретна, значит, импульс дискретен, значит и энергия дискретна. Т.е. частица в замкнутом пространстве не может иметь любую энергию, а только строго определенную.
y+ = Beikx-iwt
y- = -Be-ikx-iwt
Суммарная волновая функция y = y+ + y- = Beikx-iwt – Be-ikx-iwt = 2iBsinkx*e-iwt . Если оставить только пространственную часть, обозначить А = 2iВ, то получим волновую функцию y = A*sinkx. Ширина ящика L. Обязательно должно быть kL = np – это условие того, что на ширине этой потенциальной ямы укладывается полное число полуволн. n= 1, 2, …
kn = pn/L – только такие значения может принимать волновой вектор. Соответственно импульс может принимать значения
pn = pnħ/L
 энергия – En = p2/2m = p2h2n2/2mL2. Это уровни энергии, которыми может обладать частица в ящике.
энергия – En = p2/2m = p2h2n2/2mL2. Это уровни энергии, которыми может обладать частица в ящике.
Возьмем ящик шириной в 2А. Ангстрем – это размер атома. k=2*10-10м. Первый уровень энергии
Дата добавления: 2015-08-21; просмотров: 705;
