Прямые частного положения
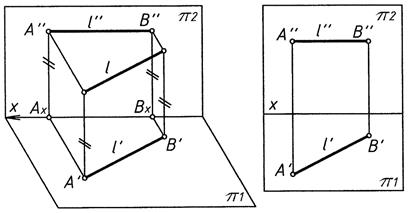
1. Прямые, параллельные одной плоскости проекций (прямые уровня) (рис. 8)
l || π1 z = const l || π2 y = const
A′′B′′ || x |A′B′| = |AB| A′B′ || x |A′′B′′| = |AB|
 | |||
 | |||
Рис. 8
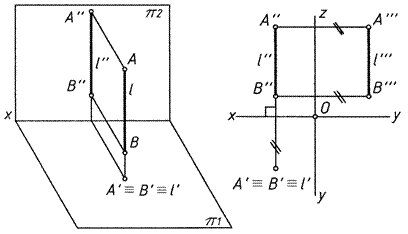
2. Прямые, перпендикулярные плоскости проекций (проецирующие) (рис. 9)
(при этом параллельны другой плоскости проекций)
l ┴ π1 l ┴ π2
 | |||
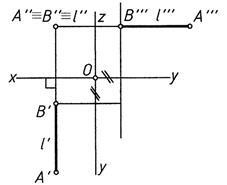 | |||
Горизонтально-проецирующая Фронтально-проецирующая
|A′′B′′| = |AB|; y = const |A′B′| = |AB|; z = const
Рис. 9
Отметим проецирующие свойства таких прямых – совпадают с направлением проецирующих прямых, на перпендикулярную к ним плоскость проекций проецируются в точку.
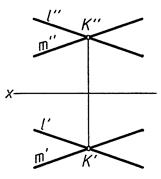
Взаимное положение двух прямых(рис. 10)
Параллельны. Пересекаются. Скрещиваются.
 l || m l ∩ m
l || m l ∩ m 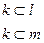 l ∙ m
l ∙ m
конкурирующие точки 1 и 2
 | |||||
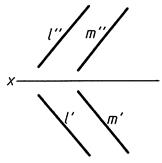 | 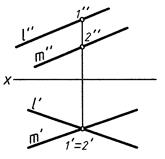 | ||||
Рис. 10
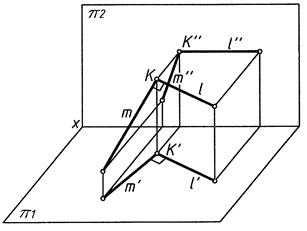
Теорема о проецировании прямого угла (рис. 11). Если одна сторона прямого угла параллельна плоскости проекций, а вторая сторона не перпендикулярна к ней, то прямой угол проецируется без искажения на данную плоскость проекций.
Дано: m ∩ l; m ┴ l; l// π1
При проецировании l′ ┴ m′
 | |||
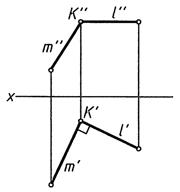 | |||
Рис. 11
Отметим, что угол между скрещивающимися прямыми равен углу между параллельными им пересекающимися прямыми.
Дата добавления: 2015-08-21; просмотров: 621;
