Определение сжимающих напряжений по методу угловых точек.

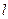Вертикальные сжимающие напряжения в точках, совпадающих с углами прямоугольника со сторонами и 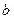, называют угловыми. Если известно угловое сжимающее напряжение, то по нему легко определяется и сжимающее напряжение в любой точке полупространства.

Вычисления упрощаются, если пользоваться таблицами значений угловых коэффициентов К_о и К_с .

Для площадок под центром загруженного прямоугольника

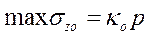(1)

Для площадок под углом загруженного прямоугольника

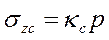(2)

где p – интенсивность равномерно распределенной нагрузки

Максимальное сжимающее напряжение будет в точках, расположенных под центром загруженной площадки. Оно вычисляться по формуле (1).

Метод угловых точек для определения сжимающих напряжений применяют в случае, когда грузовая площадь может быть разбита на такие прямоугольники, чтобы рассматриваемая точка оказалась угловой. Тогда в этой точке будет равна алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой.

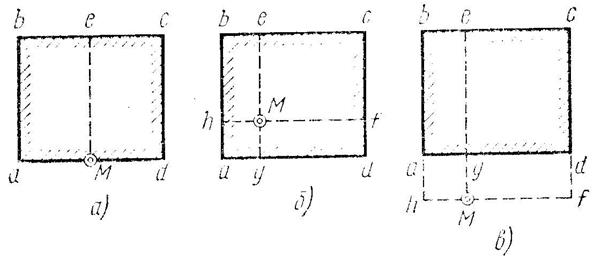
Рис 4.9 Схемы разбивки прямоугольной площади загрузки при определении напряжений по методу угловых точек

а) точка М находится на контуре прямоугольника внешних давлений

б) точка М внутри прямоугольных давлений

в) точка М вне прямоугольных давлений

В случае «а» величина определяется как сумма двух угловых напряжений, соответствующих прямоугольным загрузкам Маве и Месд

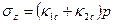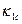, где и 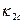- угловые коэффициенты (таблица. Цитович МН Механика грунтов)

В случае «б» необходимо суммировать угловые напряжения от 4-х прямоугольников

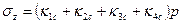
В случае «в» напряжение в точке М складывают из суммы напряжений от действия нагрузки по прямоугольникам Мhbe и Мecf, взятых со знаком (+) и напряжений от действия нагрузки по прямоугольникам Mhad и Mgdf, взятых со знаком (-), т.е.