Фазы напряженного состояния грунта

Пусть на поверхности грунта, обладающего структурной прочностью, установлен жесткий штамп, загружаемый нагрузкой N (рис. 6.1, а). Под действием этой нагрузки в массиве грунта происходят перемещения, величина которых будет возрастать по мере увеличения давления на основание. Вследствие развития в грунте дополнительных напряжений сверх ранее существовавших (от действия собственного веса грунта) он будет деформироваться. Интегральным выражением деформаций является осадка штампа S. При увеличении нагрузки осадка развивается в соответствии с кривой 1, приведенной на рис. 6.1, б.

На ней можно выделить четыре участка: ОА, АВ, ВС и СD. Участок ОА соответствует нагрузке, при которой возникающие в грунте под основной частью подошвы штампа напряжения не превышают структурную прочность грунта. При таких напряжениях развиваются преимущественно упругие осадки и осадки, связанные с затухающей ползучестью. Вследствие неравномерности распределения давления по подошве жесткого штампа напряжения под его отдельными частями (под краями), как правило, будут превышать р_str. Это приведет к перераспределению давления. Так как под основной частью штампа р<р_str, деформации будут возрастать примерно пропорционально изменению нагрузки. Эту фазу напряженного состояния грунтов в основании штампа называют фазой упругих деформаций, хотя одновременно с ними развиваются в небольших зонах пластические деформации и деформации уплотнения. Последнее обстоятельство приводит к тому, что в пределах и этой фазы между нагрузкой и осадкой нет строгой линейной зависимости.

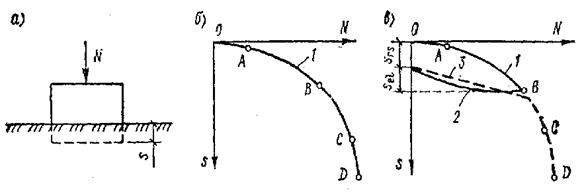
Рис. 6.1. Схема испытания грунта штампом (а) и графики зависимости осадки штампа от нагрузки (б и в).

Когда давление под всей подошвой штампа превысит структурную прочность грунта, в основании станут развиваться деформации уплотнения, которые в пределах сравнительно небольших напряжений, возникающих обычно в основании сооружения, как показывают компрессионные испытания, можно принять линейно возрастающими с увеличением давления. Если бы в пределах изменения нагрузки, соответствующей участку АВ кривой 1 (см. рис. 6.1, б), деформации уплотнения развивались в одном и том же объеме, указанный участок кривой был бы прямолинейным. Однако это не так. При давлении, незначительно превышающем структурную прочность грунта, уплотнение развивается лишь в зоне, непосредственно примыкающей к подошве штампа. По мере увеличения нагрузки грунт будет уплотняться во все большей зоне, так как в пределах все большего объема напряжения σ будут превышать структурную прочность грунта. Одновременно в грунте под краями штампа, где происходит концентрация напряжений, будут развиваться пластические деформации (деформации сдвигов), усугубляя криволинейность участка АВ.

Тем не менее при сравнительно небольших давлениях, обычно возникающих под подошвой фундаментов сооружений, кривую 1 на участке АВ можно с некоторым приближением принять за прямую. Эту фазу напряженного состояния грунтов в основании называют фазой уплотнения и местных сдвигов.

При еще большем давлении зоны пластических деформаций, развиваясь в стороны, будут приводить к уплотнению грунтов и по сторонам от этих зон, вследствие чего радиус кривизны кривой 1 на участке ВС станет меньше. Этот участок соответствует значительному развитию местных сдвигов, поэтому фазу напряженного состояния в основании, соответствующую участку ВС, назовем фазой развития интенсивных деформаций сдвигов и уплотнения, в т. ч. по сторонам от зон пластических деформаций.

Наконец, при воздействии некоторой нагрузки N на сравнительно неглубоко заложенный фундамент произойдет резкая осадка его с выпором грунта из основания в стороны и вверх (см. далее рис. 8.1). На кривой осадок появится практически вертикальная линия СВ, соответствующая фазе выпора.

Таким образом, для грунтов, обладающих структурной прочностью, можно приближенно выделить четыре фазы напряженного состояния, в условиях которых последовательно преобладают деформации: 1) упругие; 2) уплотнения и местных сдвигов; 3) интенсивных местных сдвигов и уплотнения по сторонам от зон пластических деформаций; 4) выпирания.

Поскольку структурная прочность грунта под подошвой часто незначительна, зависимость между средним давлением штампа и его осадкой (при небольшом развитии пластических деформаций), а, следовательно, между напряжениями и деформациями, принято считать линейной.

При определении напряжений в массиве грунта используются законы механики для упругого сплошного тела.Насколько грунты удовлетворяют данным требованиям?

Действие вертикальной сосредоточенной силы, приложенной к поверхности линейно-деформируемого полупространства (задача Буссинеску 1885 г.)

Рассмотрим действие вертикальной сосредоточенной силы N, приложенной в точке О к горизонтальной плоскости, являющейся поверхностью линейно-деформируемого полупространства, простирающегося в бесконечность ниже этой плоскости (рис. 6.2, а). От действия силы N во всех точках полупространства возникает сложное напряженное состояние. В общем случае в каждой точке полупространства, несколько удаленной от точки О, в декартовой системе координат будет действовать шесть составляющих 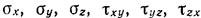. Решение этой задачи было выполнено Буссинеском (1885 г.).

Пусть положение точки М₁ (рис. 6.2, а) определяется полярными координатами R и β системы координат с началом в точке приложения силы N. Под действием силы N точка М₁ переместится в направлении радиуса R на величину S₁. Чем дальше от точки О будет расположена точка М₁, тем меньше будет ее перемещение; при R =∞ перемещение точки М₁ будет равно нулю. Следовательно S₁ можно принять обратно пропорциональным R. В то же время при одном и том же значении R для различных величин угла β перемещения точек будут неодинаковы. Наибольшее перемещение получит точка, расположенная на оси z, т. е. при β = 0. С увеличением угла β перемещения по направлению радиуса R уменьшаются, и в случае β=90° (на поверхности грунта) при малых деформациях будут равны нулю. В связи с этим можно принять, что перемещение точки М₁ по направлению радиуса, кроме зоны около точки приложения силы N, будет

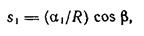
где α₁ — коэффициент пропорциональности.

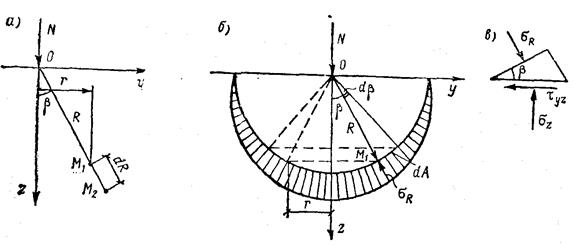
Рис. 6.2. Схема к выводу формулы (6.1)

а — расположение точек М₁ и М₂ в полупространстве; б — распределение напряжений по волушаровой поверхности с радиусом R; в — напряжения, действующие в точке М₁.

Эта зависимость удовлетворяет граничным условиям. Рассмотрим теперь точку М₂ на продолжении радиуса R. Пусть точка М₂ находится на расстоянии dR от точки М₁. Руководствуясь записанным выражением, найдем перемещение точки М₂ по направлению радиуса R:

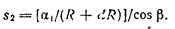
В таком случае относительная деформация грунта на отрезке dR составит:

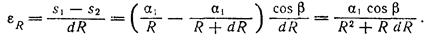
Пренебрегая величиной RdR, малой по сравнению с R², и учитывая линейную зависимость между напряжениями и деформациями, найдем выражение для напряжений сжатия, действующих на площадки, перпендикулярные направлению радиуса R, без учета силы тяжести грунта:

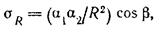(а)

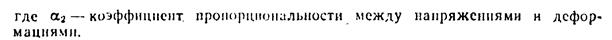
Для нахождения произведения коэффициентов α_1·α₂ отсечем мысленно часть полупространства полушаровой поверхностью (рис. 6.2, б), имеющей центр в точке О и радиус R, и составим уравнение равновесия проекций на ось z всех сил, действующих на отсеченный элемент, для невесомой среды. В таком случае получим:

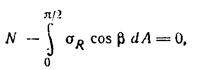(б)

где dA — площадь кольца полушаровой поверхности при изменении угла β величину dβ.

Подставив в уравнение (б) значение σ_R, определенное по выражению (а), и решив его, найдем произведение коэффициентов α_1·α₂. После подстановки значения α_1·α₂ в выражение (а) получим:

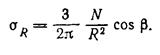
Напряжение σ_R действует на наклонную площадку dA. Рассматривая равновесие элементарной треугольной призмы (рис. 6.2, в), составим уравнение проекций всех сил на вертикальную ось:

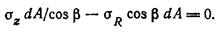
Подставив в полученное уравнение значение σ_R, по выражению (в), найдем вертикальное напряжение, которое принимается с положительным знаком при сжатии:

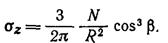
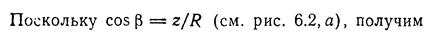
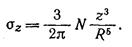
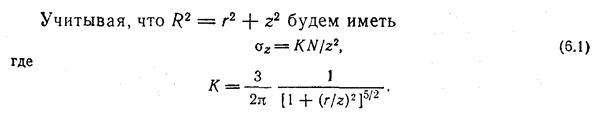
Аналогично могут быть найдены остальные пять компонентов напряжения в точке М₁.

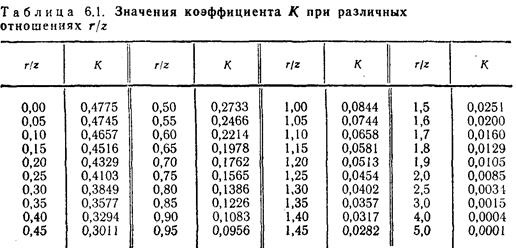
Подставляя в формулу (6.1) значение коэффициента К, найденного по табл. 6.1, определяют вертикальное сжимающее напряжение σ_Z, развивающееся в грунтах при действии сосредоточенной силы.

Определение напряжений σ_Z в массиве грунта от действия нескольких сосредоточенных сил (принцип Сен-Венана – принцип независимости действия сил)

Если к поверхности изотропного линейно-деформируемого полупространства приложено несколько сил (P₁, P₂, P₃ на рис. 6.3), то при прямой пропорциональности между напряжениями и деформациями можно использовать принцип суперпозиции и найти значение σ_Z в любой точке М простым суммированием:

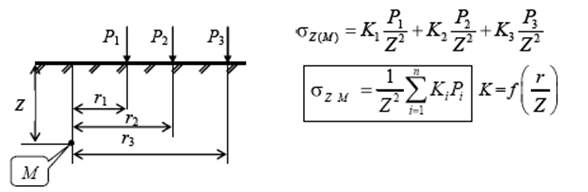
где K_i определяется в зависимости от соотношения r_i/z, причем координата z постоянна для данной точки М.

Определение напряжений σZ при действии любой распределенной нагрузки (метод элементарного суммирования)

Пусть к поверхности изотропного линейно-деформируемого полупространства в пределах площади А приложено распределенное давление (рис. 6.4, а). Загруженную площадь можно разбить на небольшие прямоугольники со сторонами b_i и l_i более сложные фигуры по ее контуру. С некоторым приближением давление, распределенное в пределах i-го прямоугольника, можно заменить равнодействующей N₁, приложенной в центре тяжести этого давления. Вертикальное сжимающее напряжение от действия силы N_i составит .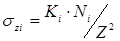

Определив величину от нагрузки каждой из небольших фигур, на которые разбита площадь А, и произведя суммирование этих напряжений, определим напряжение σ_Z от действия распределенной местной нагрузки:

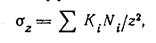
где К_i — коэффициент зависит от отношения r_i/z и берется по табл. 6.1.

Точность расчета увеличивается с уменьшением b_i и l_i.

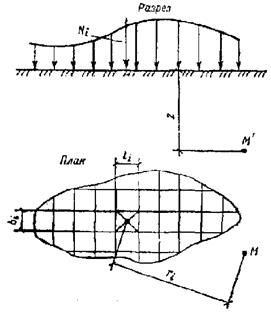
Рис. 6.4. Схемы к расчету действия любой распределенной нагрузки