Основные свойства вероятностей. Правило сложения вероятностей.
Свойства вероятностей:
1. P(A) 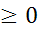
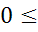 P(A)
P(A) 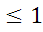
2. P(Ω)=1
Событие А+В наз-ют суммой событий А и В, если считается, что А+В происходит ó когда происходит одно из событий.
Произведение А*В-событие состоящее в том, что происходит и событие А и событие В.
Событие А и В наз-ся несовместными, если они не могут произойти одновременно. Если А и В несовместные события, то имеет место следующее равенство P(A+B)=P(A)+P(B).
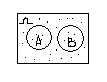
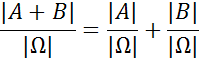
Общий случай: для произвольных А и В имеет место формула P(A+B)=P(A)+P(B)-P(A*B). Эта формула соответствует предыдущей: если А и В несовместные события, А*В не содержит ни одного элементарного исхода P(A*B)=0. Пусть А произвольное событие, тогда ч/з 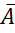 будем обозначать событие противоположно событию А, а состоит в том, что А не произошло.
будем обозначать событие противоположно событию А, а состоит в том, что А не произошло.
P(A)=1-P( 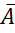 )
)
А+ 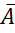 =
= 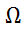
P(А+ 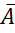 )=P(
)=P(  )=1
)=1
Если среди событий 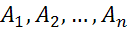 любые 2 несовместны, то P(
любые 2 несовместны, то P( 
Доказывается методом индукции на основании равенства для 2-х несовместных событий P(A+B)=P(A)+P(B)-P(A*B)

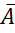 +B=A*
+B=A*  +B*
+B* 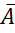 +A*B
+A*B
P( 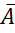 +B)=P(A*
+B)=P(A*  +B*
+B* 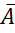 +A*B)=P(A*
+A*B)=P(A*  )+P(B*
)+P(B* 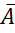 )+P(A*B)={P(A*
)+P(A*B)={P(A*  )=P(A)-P(A*B); P(B*
)=P(A)-P(A*B); P(B* 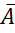 )=P(B)-P(A*B)}=P(A)+P(B)-P(A*B)
)=P(B)-P(A*B)}=P(A)+P(B)-P(A*B)

Пусть А и В, С несовместные события
P(A+B+C)=P(A)+P(B)+P(C)-P(A*B)-P(B*C)-P(C*A)+P(A*B*C)
P( 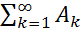 )=
)= 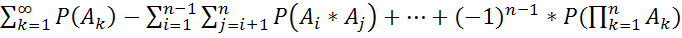
Дата добавления: 2015-06-27; просмотров: 1402;
