Отношение между событиями
А\В-это событие состоящее в том, что А происходит, а В-нет.
Свойства алгебраических операций над событиями:
1. А+В=В+А
2. А*В=В*А
3. (А+В)+С=А+(В+С)
4. (А*В)*С=А*(В*С)
5. (А+В)*С=А*С+В*С
А и В события, А 
В-событие А влечёт за собой событие В.
А=В- событие А тождественно событию В и означает А В и В А.
Система F подмножеств множества такая, что:
1. Ω 
2. если А, В , то А+В и А*В
3. если А , то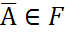 
называется алгеброй.Система F замкнута относительно операций +,*, 
-отрицание. Если система F замкнута относительно алгебраических операций над счётным числом событий, то она наз-ся σ-алгеброй.( 
)
Счётное мн-во - бесконечное мн-во м/д элементами, которого и элементами мн-ва натуральных чисел можно установить взаимно однозначное соответствие.
Аксиоматическое определение вероятностей события
Пусть F-σ-алгебра подмножеств множества Ω. Вероятностью P(A) наз-ся числовая функция определённая для всех А и удовлетворяющая 3-м условиям:
1. P(A)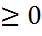 
2. P(Ω)=1
3. если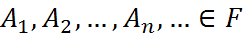 
причём 
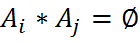для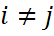 
, то P( 
)= 
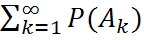
Т.обр. вероятность – неотрицательная, нормированная и σ-аддитивная функция мн-в принадлежащих σ-алгебре F.
Свойства:
1. P( 
)=0
2. P(A)=1-P( 
)
3. A B => P(A) 
P(B)
4. P(A+B)=P(A)+P(B)-P(A*B)
5. P(A+B) P(A)+P(B)
6. 
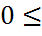P(A) 
Тройку {Ω ,F,P}, удовлетворяющую аксиомам 1-3 наз-ют вероятностным пространством случайного эксперимента.
Дата добавления: 2015-06-27; просмотров: 1108;