Корневые методы

Эта группа критериев основана на оценке качества переходных процессов по значениям нулей и полюсов Ф(p).

Пусть 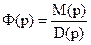, тогда разложив многочлены на множители (т.е. опред. корни).

Получим

,

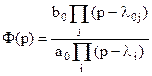λ_0j – нули ПФ, зависящие от места приложения воздействия,

λ_i – полюсы.

Заметим, что при определении устойчивости нас интересовали только λ_i. Наличие нулей существенно влияет на переходный процесс в ту и др. сторону, но методика разработана только для полюсов, т.е. для Ф(р) вида

.

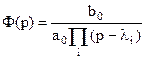В общем случае переходный процесс имеет вид:

, ,

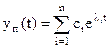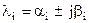т.е. переходный процесс распадается на апериодическую и колебательную составляющие.

Если найти самую длительную составляющую переходного процесса, то по ней можно дать оценку t_п, также дело обстоит с колебательностью.

1. Критерий длительности (быстродействия) – степень устойчивости η.

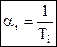Очевидно, что с уменьшением действительной части α_i переходный процесс увеличивается, т.к. растет постоянная времени апериодического звена: . Отсюда учитывая, что t_п ≈ 3T_{i max}, получим

,

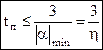где η = |α|_min – степень устойчивости (затухания).

2. Критерий колебательности – степень колебательности μ.

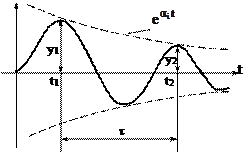Известно, то процесс описывается соотношением:

.

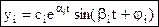Отсюда, учитывая, что sin(β_it + φ_i) = 1 в точках t₁ и t₂, получим:

- характеризует затухание (колебательность).

Здесь 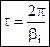- период колебаний, получается из .

Далее

,

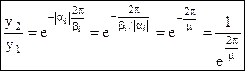где 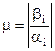- степень колебательности; .

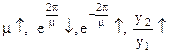Вывод: Чем больше μ, тем больше колебательность. В предельном случае μ → ∞, у₂ = у₁; а при μ = 0, у₂ = 0, т.е. реально одно колебание у₁.

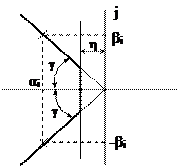
На комплексной плоскости корни 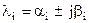определяют угол γ, откуда

.

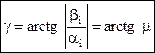Отсюда чем меньше угол γ, тем меньше колебательность переходного процесса.

Обычно величина γ используется совместно со степенью устойчивости η для задания области желаемого расположения полюсов ПФ. Она определяет допустимую колебательность и требуемое затухание переходного процесса.

Примечание: Пусть характеристическое уравнение имеет следующий вид:

.

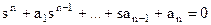Здесь 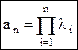, т.е. 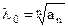- среднегеометрический корень.

По величине λ₀ можно судить о приближенном виде переходного процесса, т.е. средней длительности. Этот метод не требует определения корней.